Finding the Unique Solution of a Polar System with Variable Radius?

[Jiggerjaw]

Hello! Brand new to the forums, hopefully someone here can help me out.

Paths start out at the edge of a circle and "flow" along a polar equation that determines phi based off the initial phi (phi0) and a variable radius (ie. as your radius grows, your phi is changing). Hopefully this image can clear up the questionable wording:

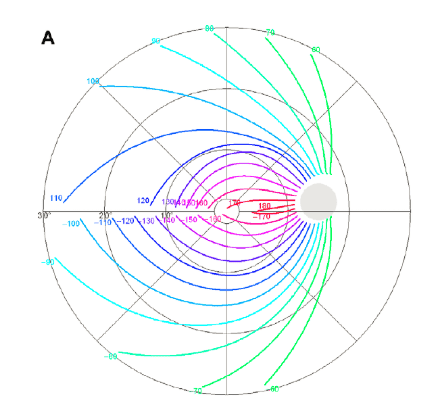
For example, for the point labelled "-100" . It's located at ~(-170 degrees, 25) but it started at whatever the initial radius is (r0) with a 100 degree "trajectory".

In reality, these aren't actually trajectories. It's just a map (axons in a human eye)... I need to figure out how to find the starting phi0 given (phi, r) and this equation:

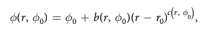
(where b and c are equations of phi0 with a different equation if r<0 or r>=0)Is this possible? I know the first step is treat it as two separate systems. One where r<0 and one where r>=0. It seems that Laplace for polar coordinates requires a fixed radius. Maybe I'm reading into it wrong though. Every video I've found on Laplace in polar coordinates is talking about signals and I'm not at all familiar with electrical engineering. I have a fairly good understanding of Linear Systems but this problem is tripping me up. I'm having trouble grasping how to work with it when there are intermediate radii between r and r0 but both r and r0 can be treated as constants since they are known values.

Sorry for the ambiguity, I'm not posting the exact equations as I'd really like to work this out on my own. Just need a push in the right direction (and hopefully not told that it's impossible).

 

[Jhoneine]

Thanks in advance!It sounds like you are trying to solve a differential equation with boundary conditions. You can use Laplace transforms to solve this type of equation, as long as you can define the boundary conditions for your system. To do this, you need to find the initial phi0 given (phi, r) and then use that to define the boundary conditions of your system. Once you have done this, you will be able to use Laplace transforms to solve the equation.

 

[soloenergy]

Hi there! Welcome to the forums. I'm not an expert in polar equations, but I'll try my best to help you out.

To find the starting phi0 given (phi, r) and the equation you provided, you will need to use the inverse function of the equation. In other words, you need to solve for phi0 in terms of phi and r.

Since you mentioned that you need to treat r<0 and r>=0 as two separate systems, I'm assuming that the equation you provided has two different forms for these two cases. So, you will need to solve for phi0 separately for each case.

For the case where r<0, you can use the inverse function of the equation for r<0 to solve for phi0. And for the case where r>=0, you can use the inverse function of the equation for r>=0 to solve for phi0.

Once you have the two values for phi0, you can compare them and choose the correct one based on the given phi and r values.

I hope this helps! Let me know if you need any further clarification. Good luck with your problem!