Finding the value of the electric charge

[arhzz]

Homework Statement

Find the value of the electric charge

Relevant Equations

F = q1q2/4pie0r^2

Hello! I am susposed to find the force of q3.The problem is given as in the picture ;

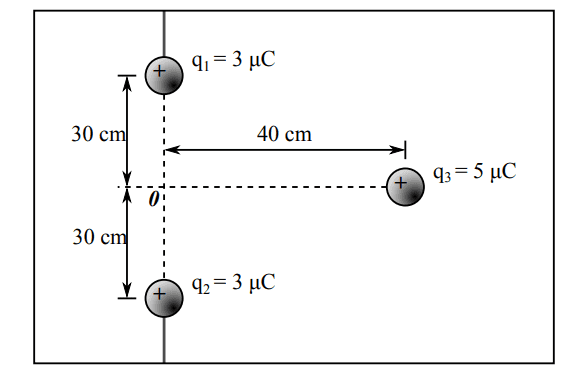
Now we are given a hint,and it says the following:
"First calculate the forces of the individual charges on q3. The superposition principle says that you can then simply add these forces vectorially
to get to the total strength."

Seems pretty straight forward.Now to get the individual forces on q3 I used this formula

$$ F = \frac{q1*q2}{4\pi e0r^2} $$ where e0 is the permatibilty constant and r is the distance between the charges. Now the distance between the charges (q1 to q3 and q2 to q3) I have calculated using Pythagoras theorem.The length of 30 cm and 40 cm should be the cathetus.

So to get the hypotenuse we simply use the formula $c^2 = \sqrt{a^2+b^2}$ I've also converted the cm to m and the distance should be 0,5m in both cases.

Now I've simply plug this into the formula F. Now $F_{23}$ and $F_{13}$ should be 0,54N (I can put the calculation in details but I don't think the problem lies here). Now to get the $F_3$ using the hint should be simply adding the forces together.I get a value of $F_3 = 1,08 N$. According to the solution sheet this is wrong.The correct solution is 0,862 N. Now I thought okay so maybe I didnt do the hint correctly.So I tried adding them and than getting the length of the vector(that should represent the hypothenuse hence the force.) So if we do that (to get the length you square them both and pull the root). I get 0,76N again not correct. Now I am kind of stumped because this seemed like an relativly easy problem and I am just not getting there.What am I missing?

Thanks!

 

[kuruman]

Wait a minute. What exactly do you mean when you say

Hello! I am susposed to find the electric charge of q3.The problem is given as in the picture ;

Charge q3 is given in the picture as 5 μC. I assume it is the resultant force that you are looking for.

After you find the magnitude 0.54 N of each force, you need to find their x and y components then add all the x-components together and separately all the y-components together using trigonometry. These two separate sums are the components of the resultant. Do you think you can do that? Note that you have two 3-4-5 triangles.

 

[arhzz]

Wait a minute. What exactly do you mean when you say

Charge q3 is given in the picture as 5 μC. I assume it is the resultant force that you are looking for.

After you find the magnitude 0.54 N of each force, you need to find their x and y components then add all the x-components together and separately all the y-components together using trigonometry. These two separate sums are the components of the resultant. Do you think you can do that? Note that you have two 3-4-5 triangles.

Oh wait of course I meant the force,bad translation on my part.I'll edit my post;

Now that is cleared up I was thinking I needd to find the x and y components of the summs.I am guessing I have to use the trig identies in some way,but not really sure how to incorporate the force into that.Also what do you mean by "two 3-4-5 triangles"?

 

[kuruman]

A 3-4-5 triangle has two right sides that are 3 and 4 units which makes the hypotenuse equal to 5 units. By the Pythagorean theorem, $\sqrt{3^2+4^2}=\sqrt{5^2}=5$. Here the unit is 10 cm and you have correctly found that the hypotenuse is 5×(10 cm) = 0.5 m.

You need to use the definitions of the sine and the cosine as ratios of the right sides to the hypotenuse. If you don't remember what they are, refresh your memory here.

 

[arhzz]

This is what I tried.Since it is a 3 4 5 triangle,and using google I got the other two angles in the triangle;

36,78 deg and 53,13 deg; (See picture below)

Now to for the first triangle(the one above the x-axis I have calculated like this.

$F_x = F*cos(36,87)$ and $F_y = F*sin(36,78 )$
Should be Fx = 0,43N and Fy= 0,32N

Now for the second 3-4-5 triangle;

$F_x = F*sin(53,13)$ and $F_y = F*cos(53,13)$

Should be Fx =0,43 N and Fy = 0,32 N

Now if we add those together vectorially, the Fx component is 0,86N and the Fy is 0,64 N.But how do I get the resultant force? I tried finding the length of the vector but I don't get the desired 0,862 N.

 

[arhzz]

This is what I tried.Since it is a 3 4 5 triangle,and using google I got the other two angles in the triangle;

36,78 deg and 53,13 deg; (See picture below)View attachment 290741

Now to for the first triangle(the one above the x-axis I have calculated like this.

$F_x = F*cos(36,87)$ and $F_y = F*sin(36,78 )$
Should be Fx = 0,43N and Fy= 0,32N

Now for the second 3-4-5 triangle;

$F_x = F*sin(53,13)$ and $F_y = F*cos(53,13)$

Should be Fx =0,43 N and Fy = 0,32 N

Now if we add those together vectorially, the Fx component is 0,86N and the Fy is 0,64 N.But how do I get the resultant force? I tried finding the length of the vector but I don't get the desired 0,862 N.

Okay so I have figured it out(finally) the y component will cancel out,while the second y component is -0,32N

See the link for an explanation(http://zonalandeducation.com/mstm/p...onents act like,vector on the coordinate axes.)

Thanks for the help!

 

[PeroK]

Okay so I have figured it out(finally) the y component will cancel out,while the second y component is -0,32N

See the link for an explanation(http://zonalandeducation.com/mstm/physics/mechanics/forces/forceComponents/forceComponents.html#:~:text=These parts of the force,is called the y-component.&text=Mathematically, the components act like,vector on the coordinate axes.)

Thanks for the help!

Basically, the force is a vector. And, in this case, the force between particles is directed along the line joining them. The first thing you should have done was drawn a vectorial diagram of the forces involved.

In your OP, you said:

Seems pretty straight forward.Now to get the individual forces on q3 I used this formula

$$ F = \frac{q1*q2}{4\pi e0r^2} $$

That is only the magnitude of the force. I would get out of the habit of writing things like that. Instead, it should be:$$ \vec F = \frac{q1*q3}{4\pi e_0r^2}\hat r $$Where $\vec F$ is the force on $q3$ due to $q1$ and $\hat r$ is the unit vector in the direction from $q1$ to $q3$.

That level of precision is important.

 

[Steve4Physics]

Hi @arhzz. A couple of points which might help you with similar problems in future.

1. Use symmetry.
The charges are symmetrical about the centre-line (x-axis). Therefore the y-components of the two forces on q₃ will cancel. No calculation of y-components is required. This means the resultant force on q₃ is simply the sum of the x-components of the two forces on q₃. And these two x-components are equal, making it even easier!

2. Learn to spot and use a 3-4-5 triangle.
3-4-5 triangles often come up. Note for example, for the smallest angle (A) of a 3-4-5 triangle, sin(A) = 3/5, cos(A) =4/5. So you don’t need to find the angle and then use sin and cos on your calculator!

 

[arhzz]

Thanks for the great advice,to both of you.I'll try to improve on the suggestions.Cheers!