Finding the Vertex Coordinates of a Rectangle In Cartesian Space

[Saladsamurai]

I am hoping to find the coordiantes of all 4 vertices when the rectangle is in any orientaion knowing the length l, the width b, the coordinate of its center mark (x_cen,y_cen), and the coordinate of vertex A as shown below:

This is NOT HOMEWORK so although I think it is possible to do, I am not sure that it is.

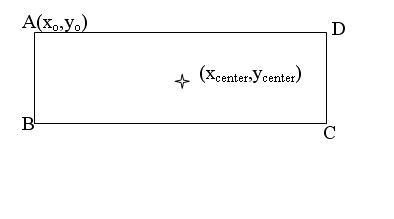
Any ideas?

I am thinking of using the vector that points from A to the center somehow... I know that if I double its length then I have arrived at the vertex C... but how to extract those coordinates, I cannot see.


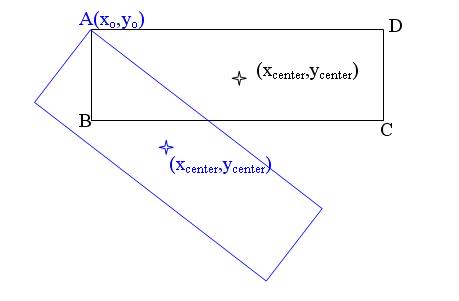
EDIT: Here is a drawing that better illustrates what I am thinking. The Blue Rectangle is the one I want to to find the vertices for. I know all information in blue.

The Black Rectangle shares the same A vertex and is in what I have DEFINED to be standard reference position (SRP).

I could find the angle of the vector that points from A to the center r_c of the black rectangle and compare it with the angle of that of the blue rectangle r'_c

I know that the difference \theta - \theta ' should be the angle that all vertices should carve out. I just can't see how to make the actual calculations of their cartesian coordinates?

 

[Saladsamurai]

Looking around online and a Rotation Matrix seems promising.

Though I am finding a lot of definitions of a Rotation Matrix, I am not finding many practical examples... so I am not exactly sure what it does.

 

[Saladsamurai]

Okay Here is where I am at: Updated Diagram for reference:

r_c and r'_c are the vectors from A to the centers.

In order for all vertices to get from the standard ref posotion to the new positions, they must all rotate through the angle phi correct?

If A=A' is locate at the point (x₀, y₀), then we have the points

A(x₀, y₀)
B(x₀, (y₀+b)) *Taking down as +Y and Right as +X
C((x₀+L), (y₀+b))
D((x₀+L), y₀)

Now to use a Rotation Matrix to get the new coordinates of A' B' C' D'
I am a little confused.

Do I use the coordinates? Or the vector components of r_BA,
r_AD, etc... ?

FOR EXAMPLE: If I am looking at the vectors r_BA and r'_BA

And I know that to get from r_BA to r'_BA I rotated through the angle Phi. How do I get the new coordiantes of B out of the deal?

 

[Redbelly98]

Hi,

While this can be done using rotations, I don't think it's necessary.

We know that B is a distance b from A, and a distance r_c from the center. In other words, it's at the intersection of two circles. You'd just need to set up the equations and solve them.

One problem I see, which is that there are two solutions for the location of B. You'll need another condition or some way to specify which solution is the desired one.