valentina
- 3
- 2
- Homework Statement
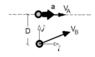
- Two players are playing football.
Player A is running in a straight line. Player B is going to pass the ball to player A with v_b constant when they're at a distance D=2m.
At that instant, player A has a velocity v_a=3m/s and he's accelerating at 12 m/s^2.
We know that the y-component of the velocity of the ball is 5 m/s.
Find the x-component of the velocity such that player A catches the ball.
- Relevant Equations
- $$x(t)=x_0+v_{x_{0}}t+\frac{1}{2}at^2$$
The first thing I did, was to find the equations for player A (p) and ball's (b) path (for each i and j component I used the equation I wrote in the relevant equations) and then I found the derivative of both equations so I could have the velocity:
$$\vec{r}_p(t)=(6t^2+3t)\hat{i}+20\hat{j} \Rightarrow \vec{v}_p(t)=(12t+3)\hat{i}$$
$$\vec{r}_b(t)=(v_{0_{x}}t)\hat{i}+5t\hat{j} \Rightarrow \vec{v}_b(t)=(v_{0_{x}})\hat{i} + 5 \hat{j}$$
Now, I tried to find the time when both paths cross:
$$(6t^2+3t)\hat{i}+20\hat{j} = (v_{0_{x}}t)\hat{i}+5t\hat{j} \iff 6t^2+3t=v_{0_x}t \land 20=5t \iff t=4s \Rightarrow v_{0_x}=27 \frac{m}{s}$$
Looking at the solution, what I did is wrong. Can someone guide me please ?
$$\vec{r}_p(t)=(6t^2+3t)\hat{i}+20\hat{j} \Rightarrow \vec{v}_p(t)=(12t+3)\hat{i}$$
$$\vec{r}_b(t)=(v_{0_{x}}t)\hat{i}+5t\hat{j} \Rightarrow \vec{v}_b(t)=(v_{0_{x}})\hat{i} + 5 \hat{j}$$
Now, I tried to find the time when both paths cross:
$$(6t^2+3t)\hat{i}+20\hat{j} = (v_{0_{x}}t)\hat{i}+5t\hat{j} \iff 6t^2+3t=v_{0_x}t \land 20=5t \iff t=4s \Rightarrow v_{0_x}=27 \frac{m}{s}$$
Looking at the solution, what I did is wrong. Can someone guide me please ?