Finding ##v## for four particles after being released from square

[ChiralSuperfields]

Homework Statement

Four identical particles, each having charge $q$ and mass $m$,
are released from rest at the vertices of a square of side $L$.
How fast is each particle moving when their distance from
the center of the square doubles?

Relevant Equations

$U_E = qV$
$KE = \frac{mv^2}{2}$

I tried solving the problem above by using conservation of energy

$U_{Ei} = U_{Ef} + KE$
$\frac{4k_eq^2}{\sqrt{2}L} = \frac{4k_eq^2}{2\sqrt{2}L} + 4(\frac{mv^2}{2})$
$\frac{2k_eq^2}{\sqrt{2}L} = 2mv^2$
$v = \sqrt {\frac {k_eq^2}{\sqrt{2}Lm}}$

However, the solutions solved the problem differently

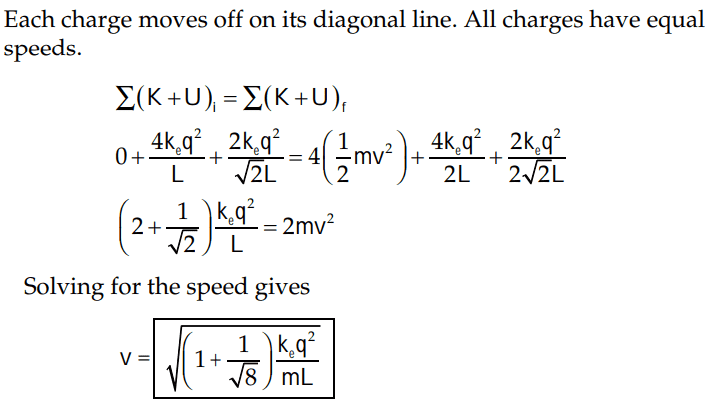
Would anybody please tell me what I have done wrong?

Many thanks!

 

[malawi_glenn]

You have not calculated the potential energy correctly. The diagonal distance is longer

 

[ChiralSuperfields]

You have not calculated the potential energy correctly. The diagonal distance is longer

Thank you for your reply @malawi_glenn !

I am centering my origin at the center of the square. Sorry, I incorrectly calculated $r$ which should be $\frac {\sqrt {2}L} {2}$ However, do you please know where they are getting the $\frac {4k_eq^2}{L}$ and $\frac {4k_eq^2}{2L}$ terms from on either side of the equation?

Thanks!

 

[PeroK]

Thank you for your reply @malawi_glenn !

I am centering my origin at the center of the square. Sorry, I incorrectly calculated $r$ which should be $\frac {\sqrt {2}L} {2}$ However, do you please know where they are getting the $\frac {4k_eq^2}{L}$ and $\frac {4k_eq^2}{2L}$ terms from on either side of the equation?
View attachment 321242

Thanks!

Where do you think they are getting them from?

 

[malawi_glenn]

However, do you please know where they are getting

Yes of course I know, but you are supposed to try to work it out yourself using our guidance. Use the geometry of a square, see picture below for a square with side lenght L. The charges are located at each corner. Focus first on the charge in the upper left corner. What is the potential in that corner generated by the other three charges (located in the other three corners)?

 

[ChiralSuperfields]

Yes of course I know, but you are supposed to try to work it out yourself using our guidance. Use the geometry of a square, see picture below for a square with side lenght L. The charges are located at each corner. Focus first on the charge in the upper left corner. What is the potential in that corner generated by the other three charges (located in the other three corners)?
View attachment 321245

Thank you for your replies @malawi_glenn and @PeroK ! The electric potential at the upper left corner is

$V = k_e(\frac {q}{L} +\frac {q}{L} +\frac{q}{\sqrt 2L})$

Where the electric potential energy is

$U_{ei} =k_e(\frac{q^2}{L} +\frac{q^2}{L} +\frac{q^2}{\sqrt 2L})$
$U_{ei} =k_e(\frac{2q^2}{L}+\frac{q^2}{\sqrt 2L})$

Many thanks!

 

[nasu]

This is not all the potential energy of the system. You understand this, right?

 

[ChiralSuperfields]

This is not all the potential energy of the system. You understand this, right?

Thanks for your reply @nasu!

I don't think I understand that. I guess the potential energy of the system is $4U_{ei}$ since $U_{ei}$ is the potential energy for a single charge?

Many thanks!

 

[haruspex]

Thanks for your reply @nasu!

I don't think I understand that. I guess the potential energy of the system is $4U_{ei}$ since $U_{ei}$ is the potential energy for a single charge?

Many thanks!

Not quite.
The EPE of two charges is a joint property. It is the energy change if one particle were to go off to infinity. Once one has gone, there is no energy change if the other does likewise.
Think how that works with more than two.

 

[PeroK]

... a useful trick is to think of an external force holding each charge in place once it has reached its final point in the configuration. This force does no work, so does not affect the PE of the system. Only the force that brings the next charge in from infinity does work.

That's the way I think about it. In fact, I learned that from @ehild several years ago.

 

[nasu]

Or you can count the energy of each pair of charges in the system. Here you have 4 charges so there are 6 distinct pairs. Four of them have the side of the square as distance and two the diagonal. If you multiply the energy obtained in post 6 by four you double count the pairs.

 

[ChiralSuperfields]

Thank you for your replies @PeroK and @haruspex !

So does that mean that a single charge configuration can be thought of has a two-charge configuration as $r \rightarrow \infty$ so the $U_e \rightarrow 0$ as it is infinitely far away from the other charge?

The first charge $q_0$ will have $\Delta U_e = 0$

Then for the next charge $q_1$ brough from infinity to $L$ distance away from charge $q_0$ then the $W = \Delta U_e$*

Where $U_{ef} = \frac {k_eq^2} {L}$

Then if the next charge $q_2$ is brough $L$ distance away from charge $q_0$ then $U_{ef} = \frac {2k_eq^2} {L} + \frac {k_eq^2} {\sqrt{2}L}$

Then for $q_3$ it must be $U_{ef} = \frac {4k_eq^2} {L} + \frac {2k_eq^2} {\sqrt{2}L}$

I guess I kind of seeing a generalization now. Really $U_e$ is just the reciprocal of the distance $r$ between each and every distinct charge pair multiped by $k_eq^2$

*I don't use the definition of work $W = Fd\cos\theta = Eqd$ since we don't know the distance from infinity to $L$ distance away from $q_0$. Actually, won't the distance $d$ be infinity, so the work done on each charge apart from $q_0$ is infinite?

Many thanks!

 

[ChiralSuperfields]

Or you can count the energy of each pair of charges in the system. Here you have 4 charges so there are 6 distinct pairs. Four of them have the side of the square as distance and two the diagonal. If you multiply the energy obtained in post 6 by four you double count the pairs.

Thank you for your reply @nasu! Sorry what do you mean count the energy of each charge pairs? I don't understand why I would multiply by 2 since there are 6 distinct pairs.

Many thanks!

 

[PeroK]

Then for the next charge $q_1$ brough from infinity to $L$ distance away from charge $q_0$ then the $W = \Delta U_e$*

Where $U_{ef} = \frac {k_eq^2} {L}$

Then if the next charge $q_2$ is brough $L$ distance away from charge $q_0$ then $U_{ef} = \frac {2k_eq^2} {L} + \frac {k_eq^2} {\sqrt{2}L}$

Okay.

Then for $q_3$ I am not sure.

Why not just use the same trick again?

*I don't use the definition of work $W = Fd\cos\theta = Eqd$ since we don't know the distance from infinity to $L$ distance away from $q_0$. Actually, won't the distance $d$ be infinity, so the work done on each charge apart from $q_0$ is infinite?

The force isn't constant! You'd have to integrate over a specified path to get the PE this way.

 

[ChiralSuperfields]

Okay.

Why not just use the same trick again?

The force isn't constant! You'd have to integrate over a specified path to get the PE this way.

Thanks for your reply @PeroK ! Thanks for sharing that trick! Sorry , I have edited post #12 after I just realized.

 

[PeroK]

Thank you for your reply @nasu! Sorry what do you mean count the energy of each charge pairs? I don't understand why I would multiply by 2 since there are 6 distinct pairs.

Your problem here is simple counting. If we have four charges A, B, C and D, then there are six pairs of interactions: AB, AC, AD, BC, BD, CD.

This gives us six terms to add together.

If there were five charges, then we would have ten pairs of interactions. Etc.

 

[ChiralSuperfields]

The force isn't constant! You'd have to integrate over a specified path to get the PE this way.

Thanks for your help @PeroK!

True the force is not constant! I guess the force to move the charge would increase the closer it got to the other positive charges.

Maybe the work may not be infinite since it would require very little work to move the charge at a near infinite distance away. However, I try to see if the integral diverges

$W = \int_\infty^L \ dx$ (assuming some component of the force applied is in x-direction)
$W = L - \infty = -\infty$

However, work should be positive since the force applied is against the repulsive electrostatic force. Do you please know what I have done wrong here?

I think maybe be something to do with absence of a coordinate system that I have defined.

Your problem here is simple counting. If we have four charges A, B, C and D, then there are six pairs of interactions: AB, AC, AD, BC, BD, CD.

This gives us six terms to add together.

If there were five charges, then we would have ten pairs of interactions. Etc.

Thanks!

 

[PeroK]

True the force is not constant! I guess the force to move the charge would increase the closer it got to the other positive charges.

That shouldn't be a guess!

Maybe the work may not be infinite since it would require very little work to move the charge at a near infinite distance away. However, I try to see if the integral diverges

It's a standard exercise to integrate an inverse square force from a finite radius to infinity. You ought to have seen that already. That's how the standard expression for EPE is derived.

As the electrostatic force is conservative, the result does not depend on the path, so you can choose a radial path to make the integral as simple as possible.

$W = \int_\infty^L \ dx$ (assuming some component of the force applied is in x-direction)
$W = L - \infty = -\infty$

However, work should be positive since the force applied is against the repulsive electrostatic force. Do you please know what I have done wrong here?

I have no idea what you are trying to do there.

I think maybe be something to do with absence of a coordinate system that I have defined.

I have no idea what that means.

 

[malawi_glenn]

First consider one pair, the upper left corner charge and the lower right corner charge.
First, they are separated by $\sqrt{2}L$ and are hold at rest, later they are separated by $2\sqrt{2}L$ and have speeds $v$.

When you have figured this out, then you can generilize this to the given problem.

 

[ChiralSuperfields]

That shouldn't be a guess!

Thanks for your reply @PeroK! Agreed!

It's a standard exercise to integrate an inverse square force from a finite radius to infinity. You ought to have seen that already. That's how the standard expression for EPE is derived.

I think have seen the EPE formula derived using that.

As the electrostatic force is conservative, the result does not depend on the path, so you can choose a radial path to make the integral as simple as possible.

I have no idea what you are trying to do there.

I have no idea what that means.

I am trying to calculate the work done to move the charge $q$ from infinity to a distance L from another charge $q$.

Do you please know how to find that work?

Many thanks!

 

[ChiralSuperfields]

First consider one pair, the upper left corner charge and the lower right corner charge.
First, they are separated by $\sqrt{2}L$ and are hold at rest, later they are separated by $2\sqrt{2}L$ and have speeds $v$.

When you have figured this out, then you can generilize this to the given problem.

Thank you @malawi_glenn ! I will have another go!

 

[PeroK]

I am trying to calculate the work done to move the charge $q$ from infinity to a distance L from another charge $q$.

Do you please know how to find that work?

1) You use the principle of superposition, which allows you to add potentials.

2) You calculate the potential relating to each charge already in place.

 

[ChiralSuperfields]

1) You use the principle of superposition, which allows you to add potentials.

2) You calculate the potential relating to each charge already in place.

Thank you for your reply @PeroK ! Sorry I should of been clearer about finding that work.

There is only once charge $q_0$ initially in the system. I am trying to find the work required to move another charge $q_1$ from infinity to a distance $L$ from that charge $q_0$.

EDIT: Actually, I think the work is equal to $W = \Delta U_e = q\Delta V = \frac {k_eq^2}{L}$, aren't it?

 

[PeroK]

Actually, I think the work is equal to $W = \Delta U_e = q\Delta V = \frac {k_eq^2}{L}$, aren't it?

Yes, although I thought we had established that already.

 

[ChiralSuperfields]

Yes, although I thought we had established that already.

Got it! Thank you for your help @PeroK !