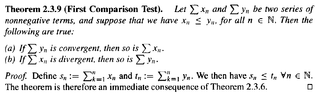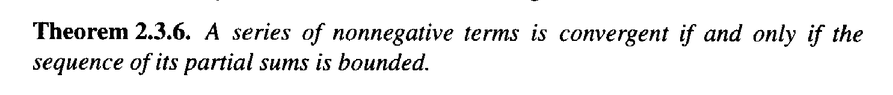First Comparison Test for Series .... Sohrab Theorem 2.3.9 ....

[Math Amateur]

I am reading Houshang H. Sohrab's book: "Basic Real Analysis" (Second Edition).

I am focused on Chapter 2: Sequences and Series of Real Numbers ... ...

I need help with the proof of Theorem 2.3.9 (a) ...

Theorem 2.3.9 reads as follows:
View attachment 9065
Now, we can prove Theorem 2.3.9 (a) using the Cauchy Criterion for Series ... as follows:Since $$0 \leq x_n \leq y_n \ \forall \ n \in \mathbb{N}$$ ... we have that ...$$\left\vert \sum_{ k = n + 1 }^m x_n \right\vert \leq \left\vert \sum_{ k = n + 1 }^m y_n \right\vert$$ ... ... ... ... ... (1)But ... since $$ \sum_{ n = 1 }^{ \infty } y_n $$ is convergent, it satisfies the Cauchy Criterion for Series ...... further ... (1) implies that $$ \sum_{ n = 1 }^{ \infty } x_n $$ also satisfies the Cauchy Criterion for Series ... ... and so $$ \sum_{ n = 1 }^{ \infty } x_n $$ is convergent ...

However ... Sohrab states that Theorem 2.3.9 (a) is an immediate consequence of Theorem 2.3.6 (see below) ... ... this means we need to establish bounds for $$ \sum_{ n = 1 }^{ \infty } x_n $$ ...... can someone please demonstrate how to do this ...
Note: If $$\lim_{n \to \infty } t_n = \lim_{n \to \infty } \sum_{ k = 1 }^n y_k = L$$ ...... does $$L$$ form an upper bound on $$ \sum_{ n = 1 }^{ \infty } y_n $$ ...... and hence also form an upper bound on $$\sum_{ n = 1 }^{ \infty } x_n$$ ...... but ... how do we prove this ... ?

Help will be appreciated ...

Peter
=======================================================================================The post above refers to Theorem 2.3.6 ... so I am providing text of the same ... as follows:View attachment 9066
Hope that helps ...

Peter

 

[Euge]

Hi Peter,

First, let's talk about Theorem 2.3.6. Recall that an increasing sequence of real numbers converges if and only if it is bounded. Given a series $\sum x_n$ of nonnegative terms, its sequence of partial sums $s_N = \sum_1^N x_n$ is increasing. Since $s_N$ converges if and only if it is bounded and the sum of a series is defined as the limit the sequence of partial sums, it follows that $\sum x_n$ converges if and only if it is bounded.

Now, let's revisit the proof of Theorem 2.3.9. If $\sum y_n$ converges, then $t_n$ is bounded, say, by $T$. As $0 \le s_n \le t_n$ for all $n$, then $0 \le s_n \le T$ for all $n$. Thus $s_n$ is bounded, which implies $s_n$ converges. In other words, $\sum x_n$ converges. This proves $(a)$. Statement $(b)$ is equivalent to statement $(a)$.

 

[Math Amateur]

Hi Peter,

First, let's talk about Theorem 2.3.6. Recall that an increasing sequence of real numbers converges if and only if it is bounded. Given a series $\sum x_n$ of nonnegative terms, its sequence of partial sums $s_N = \sum_1^N x_n$ is increasing. Since $s_N$ converges if and only if it is bounded and the sum of a series is defined as the limit the sequence of partial sums, it follows that $\sum x_n$ converges if and only if it is bounded.

Now, let's revisit the proof of Theorem 2.3.9. If $\sum y_n$ converges, then $t_n$ is bounded, say, by $T$. As $0 \le s_n \le t_n$ for all $n$, then $0 \le s_n \le T$ for all $n$. Thus $s_n$ is bounded, which implies $s_n$ converges. In other words, $\sum x_n$ converges. This proves $(a)$. Statement $(b)$ is equivalent to statement $(a)$.

Thanks for the explanation, Euge ...

Most helpful!

Peter