Rizkyffq
- 8
- 0
- TL;DR
- Flow rate of fluid at burst leakage in pipeline due over pressured
we have a project to how knowing the flow rate of fluid at the burst leakage due over pressured, probably to make it easier to understand i will attach some pictures of this mechanism.

Picture at above is simply mechanism of pipeline system that installed vertically, with fluid is mud and density of the fluid is approximation 1500 kg/m3. The pipeline system having dead end pipeline and fluids generated by particular pump. If at the end of the pipeline there is a hole/orifice/leak that covered by something and that thing will open by over pressured from fluid inside of pipeline. we intended to make the end of pipeline that having hole/orifice/leak will burst due over pressure in case to make a burst flow rate for our research.
So we design that thing covered hole/orifice/leak will broke with pressure impacted it approximation in 4000 psi, so pump will produced flow rate and makes pressure inside the pipe line until 4000 psi. If thing that covered hole/orifice/leak already broken then we close the valve so there is no flow rate produces by the pump to pipeline, in this state there is no additional fluid that distribute to pipeline.
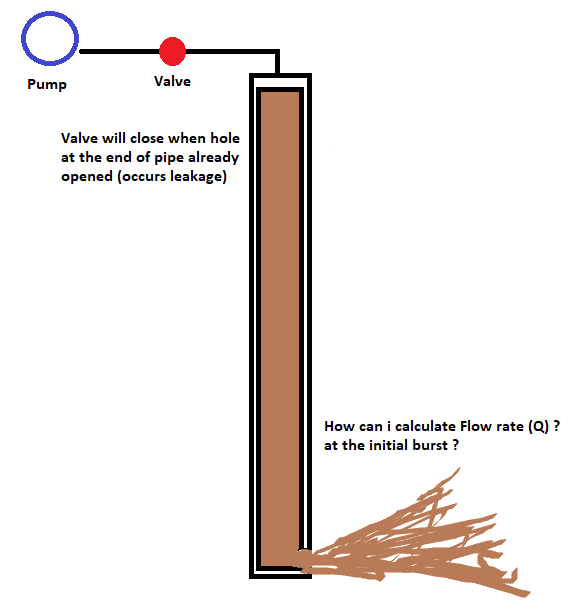
And automatically fluid inside pipeline will burst out from the pipeline with 4000 psi and because there is no additional pressure cause valve already close and pump stopped to distributing fluid then it is slowly become hydrostatic state.
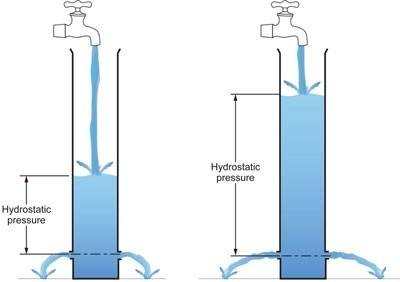
it is simple if we calculate the flow rate in hydrostatic state because we just need to know height of fluid (head), but what we confusing now is to know how to calculate the initial flow rate when burst fluid started after covered hole/orifice/leak forced opened due over pressured from the inside (4000 psi).
is it right to use this equation to calculate the burst leakage flowrate ?

and additional question :
1. When hole/orifice/leak forced opened due over pressured, is it true the pressure that in intial is 4000 psi will drop drastically in seconds towards zero (hydrostatic pressure) ? assume that outside of pipeline there is empty space so fluid that leakaged will freely flows out.
2. does Q1 = Q2 (continuity) will works in this mechanism when the first second of burst leakage happens ? so let say the Q1 is 5 litre/s from the pump then the Q2 that out from the hole is also 5 litre/s ?
Picture at above is simply mechanism of pipeline system that installed vertically, with fluid is mud and density of the fluid is approximation 1500 kg/m3. The pipeline system having dead end pipeline and fluids generated by particular pump. If at the end of the pipeline there is a hole/orifice/leak that covered by something and that thing will open by over pressured from fluid inside of pipeline. we intended to make the end of pipeline that having hole/orifice/leak will burst due over pressure in case to make a burst flow rate for our research.
So we design that thing covered hole/orifice/leak will broke with pressure impacted it approximation in 4000 psi, so pump will produced flow rate and makes pressure inside the pipe line until 4000 psi. If thing that covered hole/orifice/leak already broken then we close the valve so there is no flow rate produces by the pump to pipeline, in this state there is no additional fluid that distribute to pipeline.
And automatically fluid inside pipeline will burst out from the pipeline with 4000 psi and because there is no additional pressure cause valve already close and pump stopped to distributing fluid then it is slowly become hydrostatic state.
it is simple if we calculate the flow rate in hydrostatic state because we just need to know height of fluid (head), but what we confusing now is to know how to calculate the initial flow rate when burst fluid started after covered hole/orifice/leak forced opened due over pressured from the inside (4000 psi).
is it right to use this equation to calculate the burst leakage flowrate ?
and additional question :
1. When hole/orifice/leak forced opened due over pressured, is it true the pressure that in intial is 4000 psi will drop drastically in seconds towards zero (hydrostatic pressure) ? assume that outside of pipeline there is empty space so fluid that leakaged will freely flows out.
2. does Q1 = Q2 (continuity) will works in this mechanism when the first second of burst leakage happens ? so let say the Q1 is 5 litre/s from the pump then the Q2 that out from the hole is also 5 litre/s ?