Pressure profile of a gas flow through an orifice

[LmdL]

Hello,

The question will probably be related to mechanical engineering / chemical engineering / aeronautics. I come from the field of optics and have no background at all on fluid dynamics.

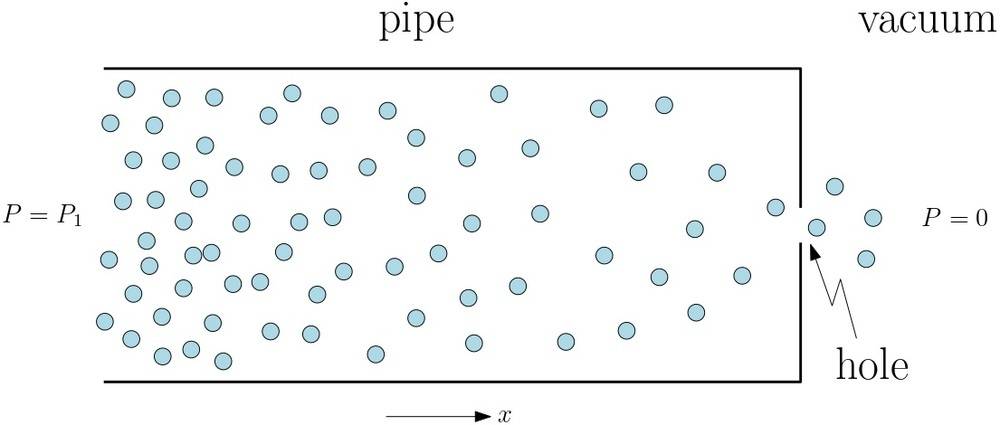
I'm trying to calculate the dependence of pressure on distance, i.e. P(x) in a gas flow problem: I assume a tube (pipe) filled with some gas (say argon), with pressure P1. At some moment, a small hole (orifice) in the pipe is opened and a gas starts to flow outside, into a vacuum (P2=0). As a result, the pressure decreases towards the hole. I want to calculate this reduction as a function of distance from the hole.
The setup is something like this:

And I want the solution P(x), like the green graph here.
From a "quick" search (that already lasts 3 days) I first found a barometric formula, but realized I have no external forces in my case to use it. Next, I found the formula that relates the pressures with the Mach number M and ratio of specific heats gamma:

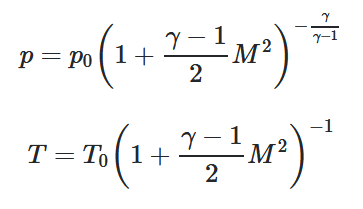
but, the Mach number is the ratio of the gas speed to the local speed of sound, and gas speeds w(x) are unknown. So, I 'm sort of came back from what I started from.
I also found a formula that relates the gas speed (w2) at the orifice to the pressures and initial gas speed (w1), volume(v1):

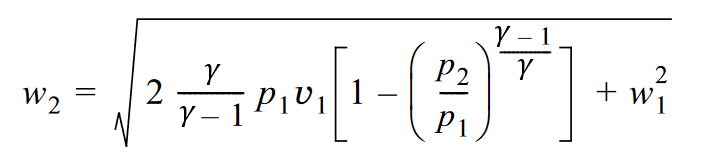
but, this gives me only one point on x axis, and this point I actually already know (it's P2, or very close to it).
I'm already after reading a couple of dozens websites on the subject, some books (Caro, Bansal, Sutton).

I appreciate any help, advice and / or suggestions where to dig in next. Thanks!

 

[jrmichler]

Your setup has two flow-related pressure drops in series. There is a friction loss in the pipe that is a function of the flow rate, and there is a flow rate through the orifice that is a function of the pressure immediately upstream from the orifice. Your sketch (nice sketch, BTW) shows that you recognize the pipe pressure drop.

To find the pressure drop in the pipe, search Moody Diagram. That diagram, with it's equation, works for any gas.

The flow through an orifice is either subsonic or sonic, depending on the pressure ratio. In your case, the downstream pressure is zero, so the pressure ratio is infinite. Your orifice flow is choked. Search choked flow through orifice to find how to calculate it. The flow rate in choked flow is dependent on the upstream gas density.

Calculate the pipe pressure drop for a range of downstream pressures. Plot on a graph. Calculate the orifice flow for the same range of downstream pressures. Plot on the same graph. The downstream pressure is the pressure immediately upstream of the orifice. The intersection of those two flow vs pressure graphs is the flow rate.

Now that you have the flow rate, you can go back to the Moody chart, and calculate the pressure at any point down the length of the pipe.

All of these calculations assume steady state flow. If you want the transient response, that starts with the initial conditions, and ends with the steady state solution found above. The actual transient response is not something you will calculate by hand.

 

[LmdL]

Dear jrmichler,
First of all, thank you very much for a quick and detailed response!
In addition, I want to record here my steps to be sure I'm not doing nonsense calculations at any step.

I went over the Moody chart that describes the friction factor as a function of the Reynolds number for different roughnesses of pipe materials.
I consider an $L = 1 \; \text{m}$ pipe of $D= 0.01 \; \text{m}$ diameter filled with Ar gas at $T = 300 \; \text{K}$ , $P_1 = 50 \; \text{torr}$ on one end and orifice ($d_2 \sim 0.1 \text{mm}$) with an exit to vacuum on the other end. Since the flow through the orifice is choked, the pressure on the second end is not really 0, but, roughly, $P_2 \sim 0.528\cdot 50 \; \text{torr} = 26 \; \text{torr}$.
Density is: $\rho_1 = \frac{M_w\cdot P_1}{R\cdot T} = \frac{40 \frac{\text{gr}}{\text{mol}} \cdot 50 \; \text{torr}}{8.3 \; \frac{\text{m}^3\text{Pa}}{\text{K}\cdot \text{mol}}\cdot 300 \; \text{K}}= 0.1 \frac{\text{kg}}{\text{m}^3}$. Ratio of specific heats for argon gas: $\gamma = 1.67$.
So, the mass flow through the orifice is
$$m_o = A_2 \sqrt{\frac{2 \gamma}{\gamma -1}P_1 \rho_1 \left[ \left( \frac{P_2}{P_1} \right)^{2/\gamma} - \left( \frac{P_2}{P_1} \right)^{(\gamma+1)/\gamma} \right]} = 1.47\cdot 10^{-7}\frac{\text{kg}}{\text{s}}$$
Q1: Here, I suppose you meant I need to obtain a set of $\left\{ m_o \right \}$ for different values of $P_1$ (pressure just before the orifice)?

Dynamic viscosity of Ar: $\mu = 2.2 \cdot 10^{-5} \; \text{Pa} \cdot \text{s} = 1.7\cdot 10^{-7} \; \text{torr} \cdot \text{s}$.
Mean velocity (required for calculation of the Reynolds number) I got according to:
$$ V_{avg} = \frac{\Delta P D^2}{32 \mu L} = \frac{(50-26) \; \text{torr} \cdot (0.01\; \text{m})^2}{32 \cdot 1.7\cdot 10^{-7} \; \text{torr} \cdot \text{s} \cdot 1 \; \text{m}} = 441 \frac{\text{m}}{\text{s}}$$
Then, Reynolds number for my case is:
$$Re = \frac{\rho V_{avg}D}{\mu} = \frac{0.08 \frac{\text{kg}}{\text{m}^3} \cdot 441 \frac{\text{m}}{\text{s}} \cdot 0.01 \text{m}}{1.7\cdot 10^{-7} \; \text{torr} \cdot \text{s}} = 1.6\cdot 10^4$$
Considering a pipe made of stainless steel ($\epsilon = 0.015 \; \text{mm}$, $\epsilon/D \sim 0.0015$) from the Moody chart I obtain a friction factor of $f_D \sim 0.028$.
Q2: Now that I have the friction factor, I can get the average flow velocity for various pressures $P_2$ (pressures just before the orifice) according to $V=\sqrt{\frac{2D\Delta P}{f_D \rho L}}$?
Q3: In case I correctly understood Q1 and Q2, I need to compare between the results obtained in them. Should I relate the mass flow and the velocity by $m_0 = \rho \cdot V \cdot A_2$, with $A_2$ beigh the area of the orifice?

Thanks again.

 

[jrmichler]

No. At the beginning, you know the pressure at the pipe inlet (P1), and the pressure at the orifice outlet (zero). You do not label the pressure at the orifice inlet, it is apparently P2. You know that P2 is less than or equal to P1, and greater than or equal to zero. You need to find P2.

You do not know the flow through the orifice until you know P2. You do not know the flow through the pipe until you know P2. You do not know P2 until you know the flow. That's why finding the flow, and P2, is an iterative process. You calculate the flow through the orifice for P2 = P1, then for a series of P2's less than P1. You calculate the flow through the pipe for P2 only slightly less than P1, then for a series of P2's increasingly less than P1. At some P2, the calculated flow through the pipe equals the calculated flow through the orifice. That's your flow, and that's the P2.

Hint: The maximum possible flow velocity in a pipe or orifice is the speed of sound. And make sure your units balance.

 

[boneh3ad]

A few questions here:

1. What is the shape of the hole (i.e. does it have straight walls or does its area change from one side to the other)?
2. Does the pipe/reservoir stay at constant pressure (i.e. is there a constant supply refilling it as it exhausts to vacuum) or does it have a finite air supply?
3. Is the pipe reservoir insulated or is heat allowed to transfer? If the latter, do you have any information about that?

Also, keep in mind this is a compressible flow, so all these traditional pipe flow calculations are, frankly, nonsense. Fanno flow is how you do friction in pipes with compressible flows.

 

[LmdL]

Dear jrmichler,
I set $P_1 = 50 \; \text{torr}$ and $P_3 = 0 \; \text{torr}$ (outside of the pipe, after the orifice). Pressure $P_2$ (end of the pipe, just before the orifice) is my variable which I set as an array running from $0$ to $50 \; \text{torr}$.
Calculation of the flow through the orifice:
I borrow the following formula:
$$\dot{m} = C_d A \sqrt{\gamma \rho_2 P_2 \left( \frac{2}{\gamma + 1}\right) ^ {\frac{\gamma + 1}{\gamma -1}}}$$
Here they suggest to use the ideal gas equation in order to eliminate $\rho_2$ (density) if it's not known directly (as in my case, as it depends on $P2$), so:
$$\dot{m} = C_d A P_2 \sqrt{ \frac{\gamma M_w}{RT} \left( \frac{2}{\gamma + 1}\right) ^ {\frac{\gamma + 1}{\gamma -1}}}$$
which, as you said, indeed depends on the upstream pressure, $P_2$.
Now, I substitute the discharge coefficient $C_d$:
$$C_d = \frac{\dot{m}}{\rho_2 A u_o} = \frac{\dot{m}}{A u}\frac{RT}{P_2 M_w} \;\; \rightarrow \;\; u_o = \sqrt{\frac{\gamma R T}{M_w} \left ( \frac{2}{\gamma +1 } \right )^{\frac{\gamma +1}{\gamma - 1}}}$$
where $u_o$ is the flow velocity through the orifice, which is now independent of $P_2$ (is that correct?). In my case, if I substitute values, I get $u_o = 180.6 \; \text{m}/\text{s}$ (which is below the speed of sound of Ar gas, $319 \; \text{m}/\text{s}$).

Calculation of the flow through the pipe:
I use the following formula:
$$\Delta P = P_1 - P_2 = f_D \frac{\rho_1 u^2_{pipe}}{2} \frac{L}{D} \;\; \rightarrow \;\; u_{pipe} = \sqrt{\frac{2 D \Delta P}{f_D \rho_1 L}}$$
with $f_D=0.028$, which gives me a range of values, depending on $P_2$:

So, since $u_o = 180.6 \; \text{m}/\text{s}$ and should be equal $u_{pipe}$, I get $P_2 = 13 \; \text{torr}$, right? What bothers me is (a) that $u_o$ is constant and doesn't depend on $P_2$ and (b) that $u_{pipe}$ according to its definition is an average velocity in the pipe, not the velocity at the other end (where the pressure is $P_2$).

Dear boneh3ad,
Answers for your questions:
1. In actual setup the orifice (hole) is about 100 microns in diameter, made in an aluminum foil. So the shape is circular and very short (thickness of a few microns) so the area of the hole is approximately the same. The pipe, if it's matter, is about 1 meter long, 1 cm diameter. The outside "vacuum" is not really 0 torr, but about 0.01 torr.
2. The left side of the pipe is at constant pressure (there is a constant supply of gas to the pipe).
3. I assume a constant temperature (gas inside the pipe and outside is at room temperature). On the exit from the orifice the gas cools (I suppose), but I don't have any information about how much it cools.
Regarding the compressibility - you are right, as it's a real gas in the end, it should be compressible. However, as I indicated in my first post, I have no background at all in fluid dynamics and it's important to me to understand the calculations at a basic, simplistic level. I will be able to account for nuances later on by myself.

Thank you.

 

[jrmichler]

OK, so let's start with some basic simplistic calculations. You have a pipe 1000 mm long and 10 mm diameter that's feeding a 0.1 mm diameter orifice. The argon enters at 50 torr, and discharges into a pressure of 0.01 torr.

The pressure drop through the orifice is less than the critical pressure ratio. The critical pressure ratio is a function of gas heat capacity ratio, but is generally somewhere near 0.5. Since your pressure ratio is much less than that, the flow velocity through the orifice is the speed of sound in argon. A quick search finds that to be about 320 m/sec.

The pipe flow area is 10,000 times the orifice flow area, so the velocity will be 10,000 times slower, or about 0.032 m/sec. The pressure drop through the pipe will be negligible. I know this from experience, but you should check it using the Moody chart.

The pressure at the entrance to the orifice is thus 50 torr, and the pressure after the orifice is 0.01 torr, so the gas velocity through the orifice is about 320 m/sec. The flow area is the orifice flow area times the orifice coefficient of about 0.6. Velocity times area times density gives you mass flow rate. The mass flow rate in choked flow does not change with changes in downstream pressure. It does change in proportion to the upstream gas density, which is linearly proportional to the pressure. So the mass flow rate in choked flow is linearly proportional to the upstream pressure.

Good search terms are choked flow and choked flow orifice. You can also search orifice coefficient, but most of what you find does not apply to your situation where the upstream diameter is 100 times the orifice diameter and the flow is choked. Look closely at the effect of the orifice leading edge radius on the orifice coefficient.

 

[LmdL]

The pipe flow area is 10,000 times the orifice flow area, so the velocity will be 10,000 times slower, or about 0.032 m/sec. The pressure drop through the pipe will be negligible. I know this from experience, but you should check it using the Moody chart.

As I understand, the mean velocity in pipe you got using the Bernoulli equation. Regarding the Moody chart, if I calculate the Reynolds number for my case (Dynamic viscosity of Ar: $\mu = 2.2 \cdot 10^{-5} \; \text{Pa} \cdot \text{s}$):
$$Re = \frac{\rho V_{avg}D}{\mu} = \frac{0.1 \frac{\text{kg}}{\text{m}^3} \cdot 0.032 \frac{\text{m}}{\text{s}} \cdot 0.01 \text{m}}{2.2\cdot 10^{-5} \; \text{Pa} \cdot \text{s}} = 1.5$$
which isn't in the Moody chart at all. Or does it correspond to the laminar flow? If so, I get a huge friction in the pipe using $f_D=64/Re$ (laminar case).

The pressure at the entrance to the orifice is thus 50 torr, and the pressure after the orifice is 0.01 torr, so the gas velocity through the orifice is about 320 m/sec. The flow area is the orifice flow area times the orifice coefficient of about 0.6. Velocity times area times density gives you mass flow rate. The mass flow rate in choked flow does not change with changes in downstream pressure. It does change in proportion to the upstream gas density, which is linearly proportional to the pressure. So the mass flow rate in choked flow is linearly proportional to the upstream pressure.

I don't fully understand how the mass flow rate through the orifice (which is as thin as aluminum foil) helps me to find the pressure vs distance graph. I'm in doubt the pressure can change so abruptly from 50 torr to 0.01 torr in only 20-30 microns of the orifice thickness. How can I be sure the significant reduction of the pressure doesn't occur before? Let's say, 100-200-500 microns before the orifice?

 

[jrmichler]

The friction factor is large, while the velocity squared is small. If you do the calculation (check your units very carefully), you should find a very small pressure drop. That tells you that P2 is approximately equal to P1, which also tells you the (lack of) pressure variation down the length of the tube.

Spend some time reading the search results for the search terms listed above, and look carefully at where and how the pressures are measured. A good rule of thumb is that the velocity at one orifice diameter (100 microns) upstream of the orifice is 0.1 times the velocity through the orifice. Since velocity pressure in subsonic flow is proportional to velocity squared, the pressure reduction at that point will be about 1%. The static pressure at 100 microns upstream from the orifice will thus be about 49.5 torr.

 

[LmdL]

Hello again,

The friction factor is large, while the velocity squared is small. If you do the calculation (check your units very carefully), you should find a very small pressure drop.

If I take a friction factor of $f_D\approx 64/Re = 64/1.5=42.7$ I indeed get, as you correctly pointed out, a negligible pressure drop:
$$\Delta P = f_D \frac{L}{D}\frac{\rho_1 u_1^2}{2} = 42.7 \frac{1 \text{m}}{0.01 \text{m}}\frac{0.1 \frac{\text{kg}}{\text{m}^3} \left( 0.032 \frac{\text{m}}{\text{s}} \right)^2}{2} = 5.7\cdot 10^{-5} \; \text{torr} \ll P_1$$
I got the idea behind it. Thank you!

Good search terms are choked flow and choked flow orifice. You can also search orifice coefficient, but most of what you find does not apply to your situation where the upstream diameter is 100 times the orifice diameter and the flow is choked. Look closely at the effect of the orifice leading edge radius on the orifice coefficient.

Regarding the orifice coefficient, I found it under "discharge coefficient" name. I found it to be around $C_d \approx 0.62$ for thin sharp-edged orifices.
Assuming pressures of $P_1 = 50 \; \text{torr} = 6666 \; \text{Pa}$ and $P_2 = 0.01 \; \text{torr} = 1.33 \; \text{Pa}$ before and after the orifice, respectively, with $\gamma \left( \text{Ar} \right) = 1.67$, $T_1 = 300 \text{K}$ and $\rho_1 = 0.1 \frac{\text{kg}}{\text{m}^3}$, I have also been able to calculate the velocity, Mach number, pressure, temperature, density, mass velocity and mass flow rate at the orifice location:
$P_o = P_1 \left( \frac{2}{\gamma +1}\right) ^{\gamma/(\gamma-1)} = 0.487 P_1 = 3246 \; \text{Pa}$ (which is larger than $P_2$, thus the flow is choked),
$T_o = T_1 \left( \frac{2}{\gamma +1}\right) = 224 \; \text{K}$ (cooling of $76 \text{K}$ relative to $T_1$),
$\rho_o = \rho_1 \left( \frac{2}{\gamma +1}\right)^{1/(\gamma-1)} = 0.65 \rho_1 = 0.065 \frac{\text{kg}}{\text{m}^3}$,
$u_o = \sqrt{\gamma R T_c / M_w} = 322.4 \frac{\text{m}}{\text{s}}$ (you was right, it equals to the speed of sound in argon gas, so Mach $M_2=1$),
$G_o = P_1 \sqrt{\frac{\gamma M_w}{R T_1}} M_2 \left( 1+\frac{\gamma-1}{2}M_2^2\right)^{-\frac{\gamma+1}{2(\gamma-1)}}= 19.335 \frac{\text{kg}}{\text{m}^2 \cdot \text{s}}$
$w_o = G_o \cdot A_o = 19.335 \frac{\text{kg}}{\text{m}^2 \cdot \text{s}} \cdot \pi \left( \frac{10^{-4}\; \text{m}}{2}\right)^2 = 1.5 \cdot 10^{-7} \frac{\text{kg}}{\text{s}}$ (which is, actually, the same number I got in my 2nd post, above).
So, I learned how to calculate different parameters at the orifice location in a choked flow.

However, I still don't understand how to produce the graph of some parameter (pressure, velocity, etc.) versus axial distance. I found some sources that produce such graphs by using one equation that relates between the Mach number and let's say pressure ($M \sim f(P_1/P)$) and another equation that relates between the Mach number and cross-sectional area of orifice/pipe ($M \sim f(A_1/A_o)$). Solution of both simultaneously gives the relation between the area ratio of orifice/pipe to the pressure change as a function of $x$, which is good, for example for de Laval nozzles, which are smoothly changing their area as a function of $x$. However, in my case, the change in the area ratio is abrupt, as I use a thin orifice, not smoothly converging/diverging nozzle. And many sources (1, 2, 3, etc.) still show that in my case there should be a smooth decrease in pressure, not abrupt one.

 

[boneh3ad]

No one here should be using Bernoulli's equation, the equation $u_1 A_1 = u_2 A_2$, or the Darcy-Weisbach equation until they've proven the flow to be incompressible. This is a compressible flow in at least some portion of the flow field, so you need to determine where and use equations valid for compressible flows. Luckily, the assumption of constant upstream pressure and an isothermal reservoir will help you considerably.

I asked about hole shape because it is important in determining the exit Mach number and the pressure required to choked the flow. If your hole expands at all after its narrowest point, you can choke it with much less pressure ratio than just a straight hole, but it sounds like your hole is most accurately modeled as a straight hole.

Because this is choked (as you have correctly suggested), you automatically know the Mach number at the narrow point (1) and the mass flow rate out of the hole depends only on the upstream total pressure and temperature, the cross-sectional area of the hole, and gas properties. You also know that, as a Mach 1 flow, compressibility is important, so you need to use equations suitable for compressible flows. I would suggest assuming isentropic flow here so you can use those relations, which will give you an alternative means for determining the Mach number upstream of the hole based on the area ratio of the pipe and hole.

The Mach number will be quite small (about 0.006), so if you want to include friction, you would therefore probably be justified to use the incompressible formulae. This will probably remain a decent approximation since friction will tend to increase the Mach number of a subsonic flow, i.e. it would be even lower further upstream. Fanno flow is the appropriate means of calculating compressible flows with friction, though it's likely to match Darcy-Weisbach fairly well at these Mach numbers. If you decrease the area ratio, though, all bets are off on that.