Fluid Dynamics - Momentum Equation for Area Change

[Magda]

Hello :)
My question concerns a control volume with a changing area. The momentum equation: p₁A₁-p₂A₂ = ṁ(V₂-V₁) is applied to the control volume.
The image shows the equation found when applying the above momentum equation to the control volume:

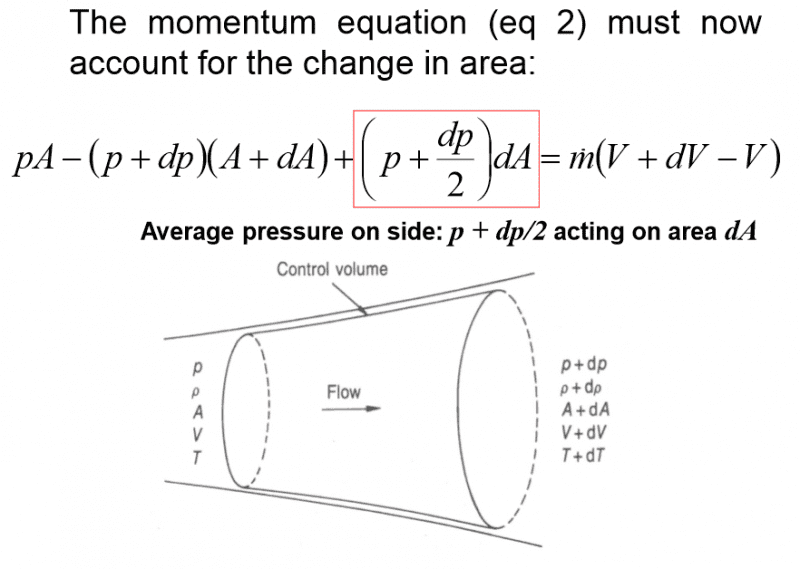
The bit I'm having difficulty with is the part in the red box, as I don't see how that part fits in with the original momentum equation. Apparently it accounts for the "average pressure on the side" but what does this actually mean? Any help in understanding this would be much appreciated.

Thanks x

 

[TSny]

Welcome to PF!
To understand the term in the red box, think about the fact that each element of area dA_s of the side of the pipe will exert a force P_sdA_s on the fluid, where P_s is the pressure at the element of area. Note that this force has a a nonzero horizontal component.

 

[Magda]

Welcome to PF!
To understand the term in the red box, think about the fact that each element of area dA_s of the side of the pipe will exert a force P_sdA_s on the fluid, where P_s is the pressure at the element of area. Note that this force has a a nonzero horizontal component.

Thank you for your response :)
I’m still slightly confused… why do I need to account for the force acting on the sides? Is it because the non-zero horizontal force component will affect the final force (term p₂A₂ in the momentum equation)?

 

[TSny]

The impulse-momentum theorem of mechanics states that the x-component of the net impulse acting on a system is equal to the change in x-component of the total momentum of the system. So, the change in x-component of momentum is due to the x-component of the net force from all forces acting on the system. The walls of the pipe exert a nonzero x-component of force on the fluid that needs to be included.

 

[Magda]

The impulse-momentum theorem of mechanics states that the x-component of the net impulse acting on a system is equal to the change in x-component of the total momentum of the system. So, the change in x-component of momentum is due to the x-component of the net force from all forces acting on the system. The walls of the pipe exert a nonzero x-component of force on the fluid that needs to be included.

ok, that makes sense. Thank you so much! x

 

[Chestermiller]

To elaborate on what TSny said, let x represent the axial position along the duct and let R(x) represent the radius of the duct at location x. The surface area of the duct upon which the pressure is acting between x and x + dx is given by $2\pi R \sqrt{(dR)^2+(dx)^2}=2\pi Rdx \sqrt{1+(\frac{dR}{dx})^2}$. The pressure acts perpendicular to the wall of the duct (Pascal's law), so the horizontal component of the pressure is given by $p\frac{dR}{\sqrt{(dR)^2+(dx)^2}}$. By Newton's 3rd law, the pressure force that the fluid exerts on the duct wall is equal and opposite to the pressure force that the duct wall exerts on the fluid. So the axial component of the duct wall force acting on the fluid in the control volume is given by:
\left(2\pi R \sqrt{(dR)^2+(dx)^2}\right)\left(p\frac{dR}{\sqrt{(dR)^2+(dx)^2}}\right)=p(2\pi R dR)=pdA

Chet

 

[Magda]

To elaborate on what TSny said, let x represent the axial position along the duct and let R(x) represent the radius of the duct at location x. The surface area of the duct upon which the pressure is acting between x and x + dx is given by $2\pi R \sqrt{(dR)^2+(dx)^2}=2\pi Rdx \sqrt{1+(\frac{dR}{dx})^2}$. The pressure acts perpendicular to the wall of the duct (Pascal's law), so the horizontal component of the pressure is given by $p\frac{dR}{\sqrt{(dR)^2+(dx)^2}}$. By Newton's 3rd law, the pressure force that the fluid exerts on the duct wall is equal and opposite to the pressure force that the duct wall exerts on the fluid. So the axial component of the duct wall force acting on the fluid in the control volume is given by:
\left(2\pi R \sqrt{(dR)^2+(dx)^2}\right)\left(p\frac{dR}{\sqrt{(dR)^2+(dx)^2}}\right)=p(2\pi R dR)=pdA

Chet

That was very useful. Thank you Chet :) x

 

[Dusan Stan]

Can I ask where is this from? I have a similar problem.

 

[Chestermiller]

Can I ask where is this from? I have a similar problem.

See the chapter in Transport Phenomena by Bird, Stewart, and Lightfoot covering Macroscopic Momentum Balances.