Fluid pressure; inclined angle

[Tclack]

I can do vertically submerged fluid force problems. One portion of my book says:
If a flat surface is immersed so that it makes an angle of $0 \leq \theta \geq \frac{\pi}{2}$ with the vertical, then the fluid force on the surface is given by:
$F=\int^b_a \rho h(x)w(x)sec\theta dx$

Can someone explain exactly what the sec(theta) is giving me; how exactly this equation changing the original equation of a vertically submerged surface. I never took trig., so please dumb it down in that area



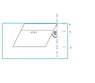
If it helps, just made a diagram. Is this the correct angle in the equation?

 

[Tclack]

ok I've found a good explanation here:
http://books.google.com/books?id=Mi...&resnum=6&ved=0CBUQ6AEwBQ#v=onepage&q&f=false

on page 490, now how does it change if we submerge a flat inclined plane further underwater, such that the top of the figure no longer "just touches" the water surface?

It would seem to me that if the figure were submerged an additional 4 feet, and our height became y+4, the sec(@) or sin@, whatever we choose our reference to be, would scew that plus 4 height

 

[Tclack]

I've tried these:

(d = additional height object is sumberged below top of fluid)
$\int^b_a \rho w(x) h(x+d)sec\theta dx$

$\rho V + \int^b_a \rho w(x)h(x+d)sec\theta dx$
(The V here being the volume of water above the submerged surface)
$\rho V + \int^b_a \rho w(x)h(x)sec\theta dx$
$\rho V + \int^b_a \rho w(x)h(x+d)sec\theta dx$


But none of them seem to work.

 

[Tclack]

Ok, i might as well come out with the problem. Please find my error:
A pool is 10 ft wide and 16 ft long, One end has a depth of 4 feet, the other end has a depth of 8 ft (therefore, the bottom of the pool makes an inclined surface) Find the Total Fluid pressure on the pool's bottom.

I can't make a picture right now, due to limitations of this computer (I'm on a Navy Ship, the computer doesn't have paint)

so basically an inclined plane submerged 4 feet.

For a visual, follow along with the last example of this:
http://www.phengkimving.com/calc_of_one_real_var/12_app_of_the_intgrl/12_09_force_exrtd_by_a_fluid.htm"
I'm following this example word for word and still missing something

I'f I go down the shallow end a height h, and follow it over to the inclined surface I get a small dh that forms a rectangle with width dw

$cos\theta = \frac{dh}{dw}$
$dw=\frac{dh}{cos\theta }$
by similar triangles, $cos\theta = \frac{4}{\sqrt{4^2+16^2}}$
$cos \theta = \frac{1}{\sqrt{17}}$
Therefore$dw= \sqrt{17} dh$------------------------(1)
now the little rectangle has an area dA such that:
$dA=dw10$ from (1): $dA=10\sqrt{17} dh$

Weight Densiy is $\rho = 62.4$ therefore,
Since Pressure is weight density x Height, the Pressure on this rectangle at depth h+4 is $\rho (h+4) = 62.4(h+4)$

Force=Pressure x Area The force dF on this rectangl is:
$dF=(62.4)(h+4)(dA)= 62.4 (h+4) 10 \sqrt{17}$

That was on ONE rectangle, to get the Total Force, take the integral
$\int^4_0 624\sqrt{17}(h+4) dh$
[itex]624\sqrt{17}(\frac{h^2}{2}+4h)\mid^4_0 [/math]
This gives me:61,747
ACTUAL ANSWER: 63,648

What went Wrong?