For a translating block with slipping find the maximum force F

[annamal]

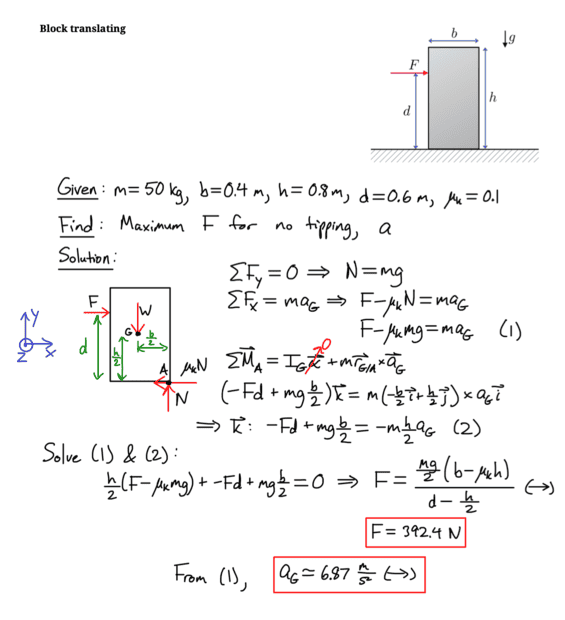
Homework Statement

For a translating block with slipping find the maximum force F to cause no tipping

Relevant Equations

Ig*alpha = sum of moments

For this translating block problem, below is the solution. I was wondering why if I took the moment about the center of gravity G, the answer for F would no longer be the same because $I_G \alpha = -\mu_k N (h/2) + N (b/2) - F*d = 0$ because $\alpha = 0$
$$F = \frac{-\mu_k mg (h/2) + mg(b/2)}{d}$$
What am I doing wrong by taking the moment about G though?

 

[TSny]

$-\mu_k N (h/2) + N (b/2) - F*d = 0$

Is $d$ the correct distance for the last term on the left-hand side?

 

[annamal]

Is $d$ the correct distance for the last term on the left-hand side?

Resolved, that was my mistake. The distance is d - h/2.