Force applied on the pulley of a system

[SakuRERE]

Homework Statement

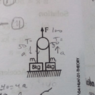
two blocks of masses 8kg and 4kg respectively are connected by a string as shown in firgure. calculate their accelerations if they are initially at rest on the floor. after a force of 100N is applied on the pulley in the upward direction (g=10 m/s).

Homework Equations

Σf=ma

The Attempt at a Solution

okay, i am used to find the acceleration for the two blocks incase the pulley is fixed (same acceleration for both masses). and i know how to find acceleration for two masses, one is hanged from fixed pulley and the other from moving pulley (a fixed = 2 a moveing). but it's my first time with this type of problem, the fixed pulley itself it moving.

now logically, the whole system will have acceleration, and i think i can find the whole acceleration for the system by considering both masses as one object being lifted (ignoring the mass of the pulley) with a force of 100N.

but How to find each block's acceleraion that's what i don't know. and i found an answer for this question which makes sense but still wasn't enough. it says:

"
force applied on the pulley will be 100 N
since pulley is ideal so we can say tension in the string must be 50 N
now we will have
for 4 kg block
plug in all values
weight of other block of mass 8kg is 80 N
its weight is more than the tension in the string so this block will remain at rest and its acceleration must be ZERO"

when i imagine it, i also end up saying block 8kg will have a=0. but i need to reach that by equations.

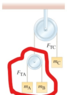
by the way, i think this system is similar to the atwood's machine which i didn't understand clearly :/ (see attachment )

 

[Orodruin]

when i imagine it, i also end up saying block 8kg will have a=0. but i need to reach that by equations.

What forces act on the 8 kg mass?

 

[SakuRERE]

What forces act on the 8 kg mass?

mmm it's the weight( m2g) down and we have the tension T up
∑ƒ= ma
m2g - T = m2a

 

[haruspex]

m2g - T = m2a

You are assuming that the 8kg mass rises, which may or may not be the case.
You are taking downwards as positive, right?
What about the other mass, and how does T relate to F?

 

[Orodruin]

m2g - T = m2a

So since mg > T, the mass will pass through the table?

 

[SakuRERE]

You are assuming that the 8kg mass rises, which may or may not be the case.

no, i am assuming mass 8kg is accelerating downwards
Umm, actually I am used to put the positive for the larger force so that for the mass 8 kg the weight is larger (assuming it goes down) and for mass 4kg it will go up so its equation is:
T- m1g= m1a1

regarding how to relate the applied force to the tension, i would say that F= 2T since the rope (string) is massless and not stretchable. so by this i will know that T= 50 N and using f=ma for each block, i will find the acceleration for m1 and m2.

So since mg > T, the mass will pass through the table?

I agree that AT THE END the block of 8kg mass will be stationary only when the block of 4kg hit the pulley but they didn't specified to find acceleration when block 4kg hit the pulley (so i was thinking of finding the acceleration while mass 8kg is still moving downwards). and here another question arises :

if the force lifting the whole system (100 N) is constant and doesn't stop, does the block 8kg still has a=0 with respect to the table?

Thanks a lot both of you

 

[Orodruin]

If the system was hanging freely, how would the 8 kg mass accelerate?

 

[haruspex]

i am assuming mass 8kg is accelerating downwards

Through the table?!

T= 50 N

Quite so. Think how that affects each mass.

 

[SakuRERE]

Through the table?!

Quite so. Think how that affects each mass.

Oh, I am sorry I forgot to mark the question as Solved.
I got it, Sir, it's just I missed the part that the string won't be able to lift the 80kg at the first place (forgive my stupidity), I mixed the concept of Atwood's machine with one movable pulley (mechanical advantage of 2) where you are able to lift things with half their weight with this situation. ( and I really don't know how it got mixed up when they are totally different systems). but thanks to everyone who kept asking me questions to think more and realize my mistakes!

thanks