Force exerted by a deflecting water jet

[issacnewton]

Homework Statement

Homework Equations

Impulse momentum theorem, Newton's second law

The Attempt at a Solution

Now the water will impart some impulse to her. Let $\bar{v_1}$ be the initial horizontal velocity of the water jet and let $\bar{v_2}$ be the final vertical velocity of the jet. Then the force exerted by the woman on the jet would be
$$ \bar{F} = r\left( \bar{v_2} - \bar{v_1} \right) $$
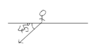
where $r = 1.2\;kg/s$ is the mass rate at which the jet is hitting her. Since $\bar{v_1}$ and $\bar{v_2}$ have the same magnitude of $6\;m/s$, we can use the Pythagoras theorem to calculate $bar{v_2} - \bar{v_1}$ and hence $\bar{F}$. Due to Newton's third law, the force exerted by the water jet on the woman will be exactly opposite in direction. So it turns out that this force will be directed at 45 degrees below horizontal as shown below. So horizontal component of

this force will be $F\cos(45)$. Using the value of $F$, this is
$$ F\cos(45) = 1.2\times 6\sqrt{2}\times \frac{1}{\sqrt{2}} = 7.2 N $$
and then using the Newton's second law for the woman, her initial acceleration would be
$$ a = F/m = \frac{7.2}{50} = 0.144\; m/s^2 $$
Is this correct so far ? For part b, I am confused. If there is a constant force impacted by the water jet, then why would the speed of the woman increase only till some maximum value ?

 

[CWatters]

What happens if she goes faster than the water?

 

[issacnewton]

What happens if she goes faster than the water?

In that case, she will lose contact with the water and no more force will be exerted by the water. So is 6 m/s her max speed ?

 

[Orodruin]

Also note that the problem is ambiguous as it does not state in which reference frame the water is deflected to go straight up after the impact.

 

[issacnewton]

Yes, you are right. I think they are assuming the ground frame.

 

[Orodruin]

There is just no way of knowing and making guesses will not leave us any closer to knowing what they intend. The ground frame would make some computational ease sense but would be less physical in my opinion. I hate it when authors of introductory level physics makes these kinds of loopholes showing their own lack of mastery.

 

[issacnewton]

so assuming that jet speed is given in the ground frame, is my conclusion correct in post #3 ?

 

[Orodruin]

so assuming that jet speed is given in the ground frame, is my conclusion correct in post #3 ?

The jet speed is clearly given in the ground frame and the conclusion is correct regardless of the assumption on in what frame the water deflects straight up.

 

[issacnewton]

Is there way to solve this problem using calculus ?. I thought since they are asking for max speed, we derive some relation of speed as function of time and then take the limit.

 

[Orodruin]

Not without making assumptions on the frame in which the water deflects straight up. The force will depend on this.

 

[issacnewton]

Ok

 

[CWatters]

The frame doesn't actually matter for this question.

They only ask for the initial acceleration in part 1). For 2) there are no other forces acting on her, eg no friction, so its trivial to calculate at what speed the net force is zero and there is no more acceleration.

It would be a different matter if they had they specified friction or similar.

 

[issacnewton]

Can we calculate velocity as a function of time here ? Initially the velocity is zero and after a log time it becomes 6 m/s, so definitely some mathematical function is there.

 

[Orodruin]

Can we calculate velocity as a function of time here ? Initially the velocity is zero and after a log time it becomes 6 m/s, so definitely some mathematical function is there.

Not without making assumptions on the frame in which the water deflects straight up. The force will depend on this.

 

[issacnewton]

Ok