Discussion Overview
The discussion revolves around the forces generated by leg muscles during walking, particularly in the context of free body diagrams. Participants explore the nature of internal forces, reaction forces, and the implications of Newton's third law in this scenario, including considerations of potential energy and inertia.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants assert that the force of the leg muscle onto the foot is an internal force and not of direct interest, while the reaction force of the ground on the foot is significant and equal and opposite to the force exerted by the foot on the ground.
- There is a question regarding what force causes the leg muscle to exert force onto the foot, with some suggesting that this is also an internal force.
- One participant emphasizes that causation does not influence Newton's third law, stating that it is arbitrary which force is considered the action or reaction.
- Another participant introduces the idea that the inertia of the body and changes in potential energy are relevant to the discussion, although others clarify that these are not forces in the context of Newton's third law.
- Mathematical expressions are introduced to clarify the relationship between potential energy and force, with a focus on the gradient of potential energy.
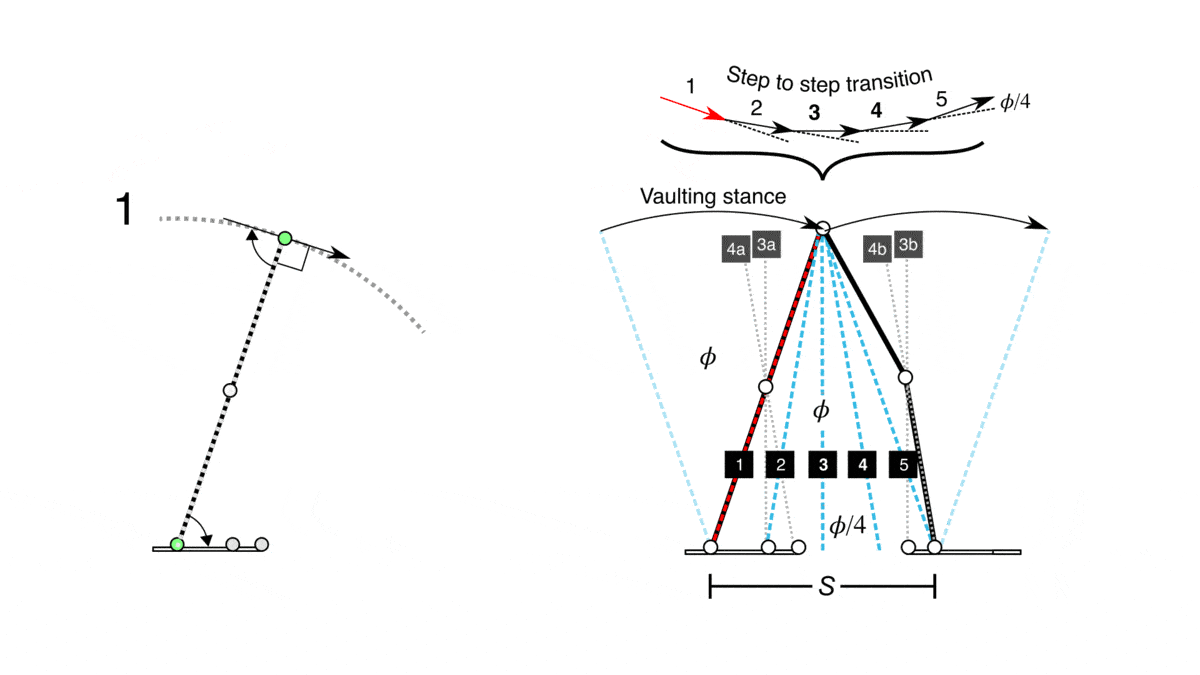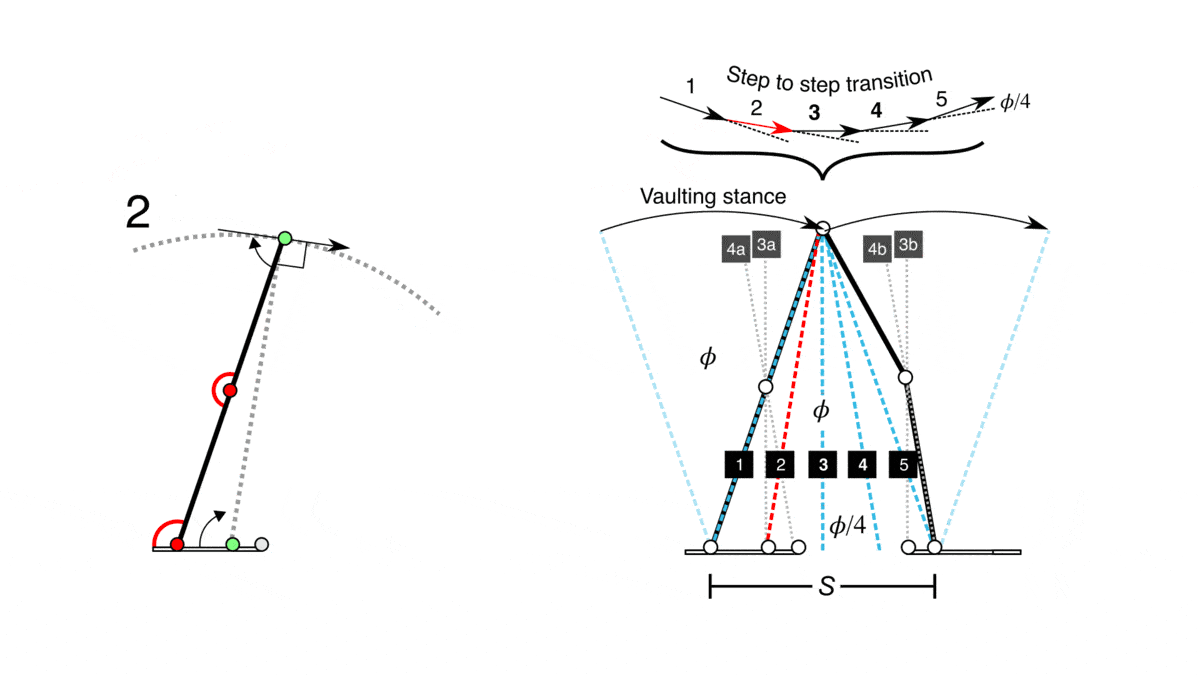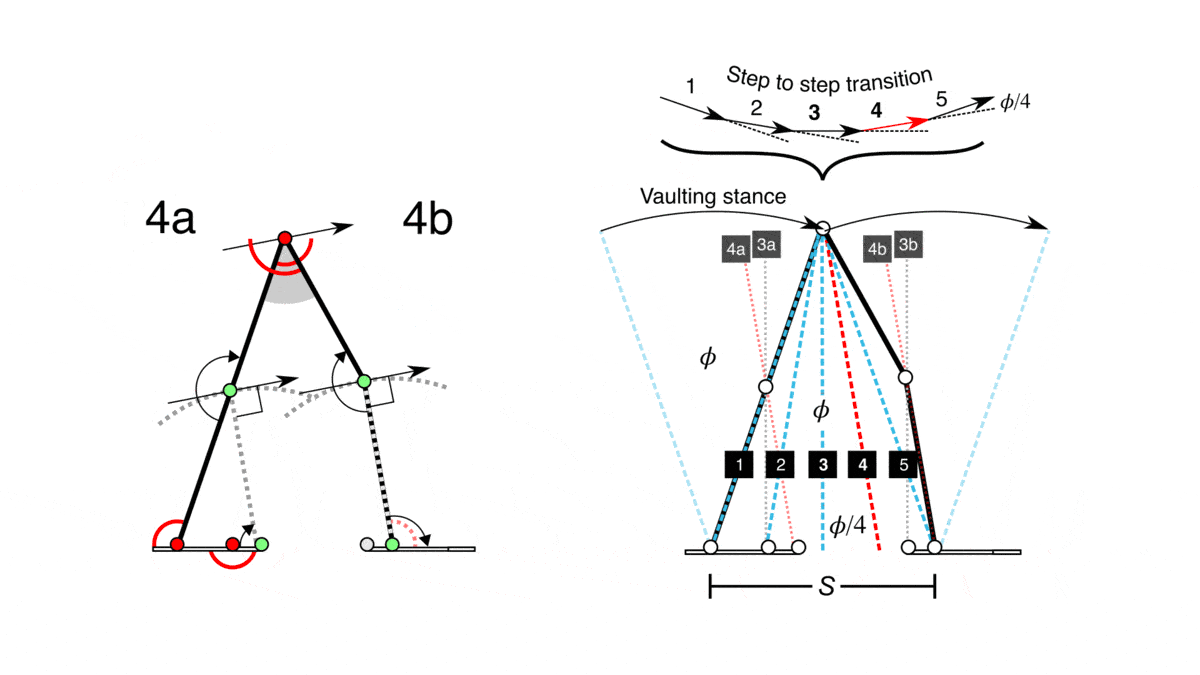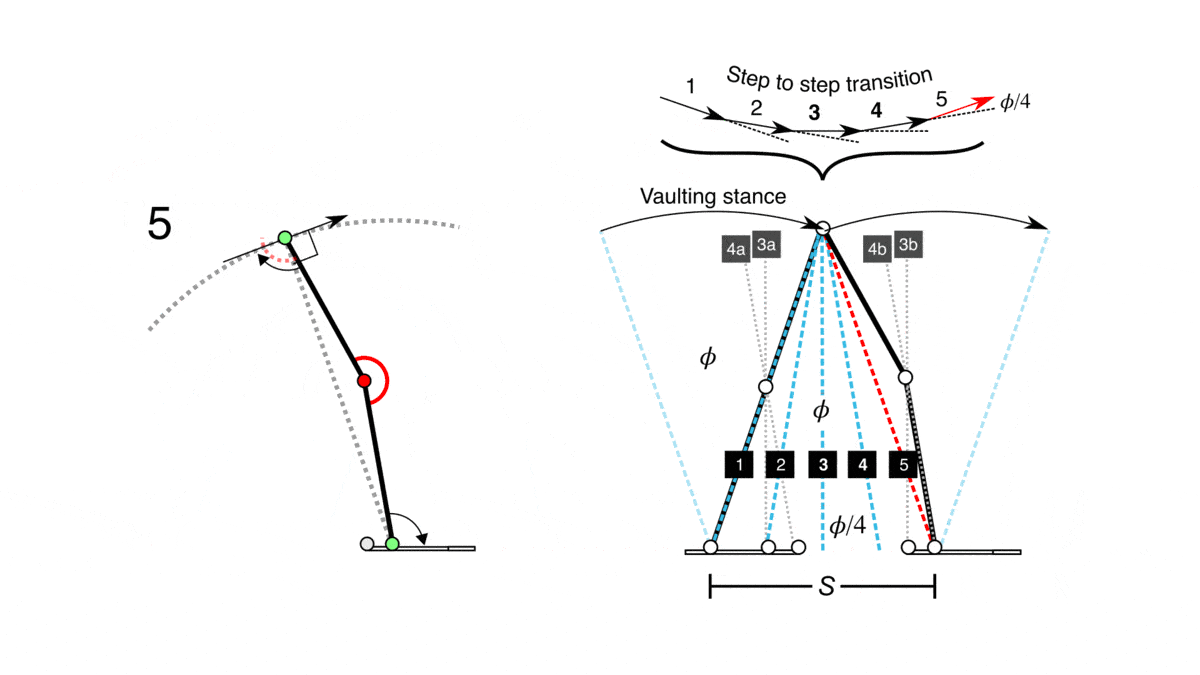
- There is a mention of the mechanics of walking, including the role of ligaments and muscle actions in propelling the body forward.
Areas of Agreement / Disagreement
Participants express differing views on the relevance and interpretation of internal forces, the application of Newton's third law, and the definitions of forces in relation to potential energy and inertia. The discussion remains unresolved with multiple competing perspectives.
Contextual Notes
Some statements rely on specific definitions of forces and may not account for all assumptions involved in the discussion of internal versus external forces. The mathematical relationships presented may depend on the context of the physical scenario being analyzed.