Force of impact (ladder to head)

[Kyrre Hovda]

Hi everyone!

need to calculate the impact force done by the ladder to the head explained in the drawing. Can anyone help?

Kyrre

 

[PeroK]

Hi everyone!

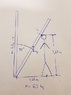
need to calculate the impact force done by the ladder to the head explained in the drawing. Can anyone help?

Kyrre

Are you talking about holding the ladder up using your head or letting the ladder fall onto your head?

 

[Kyrre Hovda]

Hi PeroK,

the ladder is falling onto the head

 

[PeroK]

Hi PeroK,

the ladder is falling onto the head

The force depends on the rigidity of the ladder and your skull. If the ladder had a thick foam coating, then that would reduce the impact force. It also critically depends on how much you are able to move during the impact. If you stand rigidly then there will be a much higher force than if you bend your knees as the ladder strikes.

 

[Kyrre Hovda]

The force depends on the rigidity of the ladder and your skull. If the ladder had a thick foam coating, then that would reduce the impact force. It also critically depends on how much you are able to move during the impact. If you stand rigidly then there will be a much higher force than if you bend your knees as the ladder strikes.

The ladder is made from aluminium. Assume the head doesn't move much during impact.

 

[PeroK]

The ladder is made from aluminium. Assume the head doesn't move much during impact.

That data is just as important as the mass of the ladder or the height of the person. You would need to measure the movement of the head during the impact to determine the force. If the head doesn't move at all, then the force tends to an infinite force.

 

[Kyrre Hovda]

That data is just as important as the mass of the ladder or the height of the person. You would need to measure the movement of the head during the impact to determine the force. If the head doesn't move at all, then the force tends to an infinite force.

Lets say the head moves 5 cm. How do you calculate the force?

 

[PeroK]

Lets say the head moves 5 cm. How do you calculate the force?

I take it this isn't homework, but an accident investigation of sorts?

How much physics do you know? Do you know what angular momentum is?

 

[jbriggs444]

Given the distance moved by the head and the [questionable] assumption that the force is constant over that distance, one can immediately come up with a rough estimate of the force involved. The strategy is to start by computing the kinetic energy of the ladder and then equate that to the work done in stopping the ladder.

The kinetic energy of the ladder can be determined most easily by equating its kinetic energy [rotational or otherwise] with its loss of potential energy.

 

[russ_watters]

"Force of impact" isn't really a thing. You can fake some numbers and calculate a force, but it will seem really large while not being very meaningful.

Impacts are generally measured in momentum or energy: such as the energy required to break a metal bar...or bone. Try googling "fracture energy" and "charpy impact test".

 

[Kyrre Hovda]

I take it this isn't homework, but an accident investigation of sorts?

How much physics do you know? Do you know what angular momentum is?

Yes, it was an accident. I have calculated the angular acceleration using the equation in the piqture. And the angular speed at 35 degrees.

 

[Kyrre Hovda]

Thanks for all replies folks! And bear in mind i might be using some words at bit imprecisely, since I'm norwegian :P

 

[PeroK]

Yes, it was an accident. I have calculated the angular speed using the equation in the piqture.

As suggested by @jbriggs444 above, there is a shortcut simply by considering energy. The force acting over the distance (e.g. $d = 5cm$) must equal the kinetic energy lost by the ladder. And the kinetic energy of the ladder is equal to the gravitational potential energy lost.

Approximately, therefore, the force is given by $F = \frac{mgh}{d}$, where $h$ can be calculated from the length and angle of the ladder:

$h = \frac{L}{2}(1 - \cos \theta)$

Although, quite what this calculation means in physical terms is not clear.

Note: if you assume that the angle you have is the final angle, then that takes care of any additional PE lost in the collision itself.

 

[Kyrre Hovda]

As suggested by @jbriggs444 above, there is a shortcut simply by considering energy. The force acting over the distance (e.g. $d = 5cm$) must equal the kinetic energy lost by the ladder. And the kinetic energy of the ladder is equal to the gravitational potential energy lost.

Approximately, therefore, the force is given by $F = \frac{mgh}{d}$, where $h$ can be calculated from the length and angle of the ladder:

$h = \frac{L}{2}(1 - \cos \theta)$

Although, quite what this calculation means in physical terms is not clear.

Note: if you assume that the angle you have is the final angle, then that takes care of any additional PE lost in the collision itself.

I have calculated the kinetic energy. Again see the picture :P

 

[PeroK]

I have calculated the kinetic energy. Again see the picture :P

That was the hard way. In any case:

$Fd \approx \Delta KE$

 

[jbriggs444]

$h = \frac{L}{2}(1 - \cos \theta)$

Although, quite what this calculation means in physical terms is not clear.

The first two terms in the series expansion of $\cos \theta$ yield $1 - \frac{\theta^2}{2}$. This means that for "small" rotations, the 1's cancel and you have a kinetic energy scales as the square of the lean angle at impact.

 

[berkeman]

Thread closed for Moderation...

 

[anorlunda]

Thread will remain closed. PF can not provide accident analysis to be used for legal purposes.

The OP is urged to hire a professional for accident analysis.