Forces, 3 masses, 2 by Tension, constant A

[Albertgauss]

Hello,

This is an advanced forces problem from introductory Calculus with Physics.

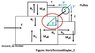
I have mostly solved the problem I am posting here but am just missing a force on my diagram somewhere. M. The jpeg below "MassCartTheProblem_1.jpg" shows a picture of the situation and the goal is to find the constant acceleration. There are three masses, ([M][/B], [M][/1], [M][/2]. There is a force F applied to the right and the goal is to find the accelerations everywhere, assuming the two masses connected by the tension do not accelerate with respect to the big block. No friction anywhere, pulley is massless.

The problem is that I know that the answer should be

F = ([M][/B] + [M][/1] + [M][/2] )a but I only come up with F = ([M][/B] + [M][/2] )a

Somehow, the mass on top of the block is not making its way into the final "F = ma". Of course, I know that if the whole system moves together, the system behaves as one big block of [M][/B] + [M][/1] + [M][/2]. However, I cannot find any other forces further than what I drew in figure "MassCartForces_2.jpg". I provide Newton's Laws for these forces for each mass in each direction in the figure "MassCartEquations_3.jpg. I cannot find a way to draw some other force in "MassCartForces_2.jpg" that couples the [M][/1] term into equation 7) on the figure "MassCartAlgebra_4.jpg".

One explanation I came up with is that maybe when [N][/B] pushes on [M][/2], [N][/B] is not the only force in the x-direction acting on [M][/2]; that is, perhaps since [M][/1] and [M][/2] are connected, there is some inertia of [M][/1] transmitted through the cable. I drew this "horizontal tension" in the figure "HorizTensionMaybe.jpg". If I do this, I can put another term in equation 7) of figure "MassCartAlgebra_4.jpg" by using equation 2) of the figure "MassCartForces_2.jpg".

If the above is wrong, can anyone show me how to draw the subtle missing force on the force diagram that will make the equations on "MassCartEquations_3.jpg" yield the correct
F = ([M][/B] + [M][/1] + [M][/2] )a ?

 

[jbriggs444]

What forces act on the pulley? If it is massless, what must be true about the vector sum of all forces acting on the pulley?

 

[scottdave]

What forces act on the pulley? If it is massless, what must be true about the vector sum of all forces acting on the pulley?

I had the same thought. The pulley is exerting a force to change the direction of the tension force, so there must be a force in the opposite direction (on block B maybe?)

 

[jbriggs444]

Yes, I would assume that the pulley is somehow rigidly mounted to block B.

 

[Albertgauss]

Yes, the pulley is rigidly mounted to Block B. Sorry about that; I didn't draw in the rigid connection from block B to the axis of the pulley. I revised this in the attached figure, "PulleyActionReaction.jpg". Anyway, does the below have what you maybe have in mind for a possible action/reaction force on the pulley and [M][/B] connected by the line adjoining the Pulley and Block? (Components are shown in blue, magnitude in Green). The pulley is massless and assumed not to rotate, so T = T'. Thus, would you say that T' vertically upwards and acting on Block B doesn't affect the vertical equations of Newton's Laws to change the overall equations of earlier, so that checks out. If T = T' , Then I would have, for the horizontal equation of Newton's Laws on Block B

F + T' - [N][/B] = [M][/B]*a. Plug in for T' = T, we have F + [M][/1]*a - [N][/B] = [M][/B]*a. Plug in [N][/B] = [M][/2]*a
and this gives
F + [M][/1]*a - [M][/2]*a = [M][/B]*a

but now the sign on [M][/2]*a is not correct. I'm still missing something.
.

 

[jbriggs444]

F + T' - [N][/B] = [M][/B]*a

Please justify that equation. Where do you see a force of magnitude T' acting on mass B in the horizontal direction?

 

[Albertgauss]

Please justify that equation. Where do you see a force of magnitude T' acting on mass B in the horizontal direction?

I circled that T' in the attached picture. As I understand it, you have to add up all the forces in the X-direction, for this part, on Block B. The forces in the X-direction on block B would be

F (points to the right, hence positive)
[N][/B] (points to the left negative)
T' (hypothesized right now, but would point to the right and would also therefore be positive)

SInce Block B accelerates to the right, the overall [M][/B]a would positive and to the right, since F and T' would be larger than [N][/B].

In equation form: F - [N][/B] + T' = [M][/B]a

I feel like the pulley---in the top right side of it---feels tensions to the left and down due to the actual cable connecting [M][/1] and [M][/2] masses. But I'm not sure if Block B is feeling T' the way I have drawn it, (i.e., pushing the pulley out of the way as [M][/B]) moves or is feeling the pulley as some kind of inertia Block B feels it is running into (in which case, the signs on T' on block B would flip). I had thought maybe that [M][/1] and [M][/2] could form a rigid object all on their own, and in that case we would have

[N][/B]= ([M][/1] + [M][/2])a. But then, I wouldn't need the tensions to be a part of the original problem.

 

[jbriggs444]

I circled that T' in the attached picture.

I apologize. I lost track of which was block B under the clutter of arrows. You have that T' drawn as a rightward force acting on block B. Was that your intent?

 

[Albertgauss]

" You have that T' drawn as a rightward force acting on block B. Was that your intent?"

Yes, though I'm not sure if its right. If it was flipped, I think everything would work out, but flipping that T' doesn't seem right to me somehow.

 

[scottdave]

So you should have horizontal forces acting on block B of (magnitude T'), and Nb and the external force F.

 

[jbriggs444]

" You have that T' drawn as a rightward force acting on block B. Was that your intent?"

Yes, though I'm not sure if its right. If it was flipped, I think everything would work out, but flipping that T' doesn't seem right to me somehow.

In which direction does the force from block B need to act on the pulley to keep the pulley in place? In which direction, then, must the force from the pulley on block B act?

 

[Albertgauss]

I think the following does make sense. It may be complicated how all the forces work their way through reaction pairs to Block B from the pulley, but it does seem correct to me that, if I had a rope pulled on the pulley as in this problem, that action would transmitted to Block B, resulting in the tensions in the circle red as indicated below. The following arrangement of forces does give the correct answers for the equations. I feel satisfied here that my question is answered, unless anyone else has anything to add.

 

[haruspex]

I think the following does make sense. It may be complicated how all the forces work their way through reaction pairs to Block B from the pulley, but it does seem correct to me that, if I had a rope pulled on the pulley as in this problem, that action would transmitted to Block B, resulting in the tensions in the circle red as indicated below. The following arrangement of forces does give the correct answers for the equations. I feel satisfied here that my question is answered, unless anyone else has anything to add.
View attachment 205773

Looks good.