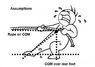
CWatters said:
the 300N friction force is shared by both feet.
... some of the excess torque generated by his mass must be supported by his rear foot
...(which is under his COM)
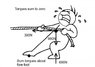
... friction force is shared in proportion to the load on each foot then the friction force on each foot is
...Rear..300* 680/980 = 208N
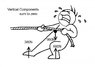
..So now we have horizontal and vertical components for the force on each foot...
Rear..Vertical = 680N...Horizontal = 208N
CWatters said:
1)...and his COM being over his rear foot etc.
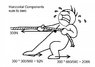
4) The fourth diagram shows the horizontal components. I have made the reasonable assumption that the 300N friction force is shared in proportion to the vertical load on each foot. That
92 + 208 + (-300) = 0 √
... Note that the total force acting on each foot acts at about 73 degrees to the horizontal. There is no reason why this should be 45 degrees. .
CWatters said:
PS: Some may question my assumption about the way the friction force is shared by each feet
You may be right, but your basic assumption that LF is bang under the COM and consequently g is transmitted
entirely on the back foot.
This situation is unrealistic because if you are pulling (and being pulled, let's not forget that the truck is in itself
a simplification of the original problem:tug-og-war') CM is continuously moving , adjusting itself to the torque (sometimes instinctively or authomatically).
If one foot is under CM you can transmit all your weight on your left leg
if no other force is acting on you, you can lift your right foot from the ground and then adjust your posture so that CM is aligned with the center of the left foot. (Position B)
gravity A-B
I have followed DaleSpam advice and started from the simplest position: no rope. Here is my sketch:
Position B
If the rear foot is at B the whole weight is on the LF, and no g is acting on RF, you may lift it and nothing happens.But, if it is
beyond B (at A, or further) the weight is shared in growing proportions by RF.
When you are pulling the rope, the appropriate position of CM/lF is found authomatically, pushing against the block at the required force. Here are the forces necessary to compensate a pull of 300 N:
Position A
As you can see there is a
horizontal F-x on RF (-88N) which is opposed by the Block pinned to the ground (do you call this 'friction'?) and a
positive Fx from gravity on LF
(DaleSpam disagrees but any civil engineer will confirm that a weight on sloping supports (and the legs are sloping here) generates a horizontal normal push/ force). In the sketch it's 148N but it can vary and adjust itself to needs) .This x-force will anyway compensate the -x force you supposed will produced when you pull on the rope.
I figured an angle of 10°-15° for LF, but I am not sure when 148 is right. What we know for sure is that the R-leg angle
must be 45°, at least as a starting point, else we would be introducing too many variables.
If G on LF 856N, the left foot will gain the necessary 124 N missing to reach the balance (-88-212) the horizontal F-x which is necessary to compensate the torque fom the rope +300N.
If you agree on this A diagram, I'll show you the next step, when there is tension on the rope.
If you had enough, I thank you for your invaluable help that has guided me in this tangled issue.