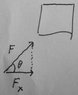Forces involved in a 'tug of war'

[CWatters]

I am saying that just standing on ice or on a waxed floor and with your legs astride at an angle of less than 45/35°, you will see that there is a horizontal pull on your foot.

The effect you refer to ONLY exists because the human body is NOT RIGID. There is a hinge at the hips. If the man was rigid there would be no apparent horizontal force at the feet.

It is difficult to account for this effect. How rigid is he? The hinge at the hips cannot be totally free to move or he would fall.

Edit: I agree with this reply by A.T...

The legs are rotated apart because the vertical forces on your feet create a troque around the hip. There are no horizontal forces pulling the feet apart.

 

[Dale]

Pardon my ignorance, DaleSpam, but a torque on hip does not mean that your foot is pushed outward?

A bending moment on the hip means that the leg is rotated outwards. In this case the outward rotation is caused by an upwards force at the foot, not a horizontal force.

Is this what you meant 1 foot?

Yes, but again you have all sorts of extra forces that don't belong on the diagram (forces that the man exerts on other things) and again you have given gravity a horizontal component that it does not have.

What is the force of gravity acting on the two legs? (and on the block)?

For at least the 3rd time, gravity acts at the center of gravity by definition, and it acts vertically downwards at that point.

 

[Dale]

if I forget to properly spread the sides,as soon as I mount they are immediately pushed apart.

They are not pushed outward by a horizontal force at the floor, they are rotated out by the bending moment from the vertical force at the floor.

In fact, under normal conditions the horizontal friction force at the floor will cause an inward torque, not an outward one. In the case of a frictionless floor the bending moment is entirely due to the vertical normal force.

Now if this is true, can you explain to me what is the difference between a ladder and a leg? Why doesn't a leg behave like a ladder?

A leg behaves exactly like a ladder for this purpose. You are misunderstanding the forces acting on a ladder in the same way you are misunderstanding the forces acting on a leg. Specifically, for both you are mistakenly assuming that an outward bending moment at the hip/hinge implies a horizontal force at the foot.

 

[bobie]

The scenario that I suggested as being the simplest was to have only one leg. It is not a tug of war without a rope, but you certainly could have a one-legged tug of war.
.

Is this what you meant?
http://s47.photobucket.com/user/lisa0rg/media/T2_zps18695702.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0
I considered 300 and 750 N to simplify it.

If these are torques , like in a pendulum?, they act tangentially or perpendicularly?
Please , anyone give me the correct values for the three notes ((1),(2),3)) this would help me most.

If the forces were equal 300 and 300 we would have equilibrium, and applying the parallelogram I would find the force on the pivot = 424. But if I use it here instead of a square I get a 2.5:1 rectangle and the resulting force is at 68°, how do I find the force acting on the pivot, here?
Can you, also, tell me how to use signs, shall I follow the cartesian axes or what?

Thanks for your comprehension

 

[A.T.]

If these are torques , like in a pendulum?, they act tangentially or perpendicularly?

For a 2D problem the torques act clockwise or counter-clockwise depending on their sign. Technically they are vectors perpendicular to the 2D plane you are analyzing:

http://en.wikipedia.org/wiki/Torque

 

[bobie]

For a 2D problem the torques act clockwise or counter-clockwise depending on their sign. Technically they are vectors perpendicular to the 2D plane you are analyzing:http://en.wikipedia.org/wiki/Torque

In the diagram the CM is the hip and is subject to a torque, if there where no pivot the vertical g would pull the (leg) to the left but since ther is a pivot, it must follow a circle. Now,

- Are the tangential values in the image exact?
- And, what are the correct values for the forces at the notes (1,2,3) ?

These answer can hel me more than any link. I read those articles, but I cannot apply the principles to a particular example (yet)

 

[Dale]

Is this what you meant?
http://s47.photobucket.com/user/lisa0rg/media/T2_zps18695702.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0
I considered 300 and 750 N to simplify it.

This is very close, but it is even simpler than what you drew. There should only be three arrows on the diagram. The red vertical arrow is the force of gravity on the man, the blue horizontal arrow is the rope tension pulling on the man, and the green diagonal arrow is the ground reaction force on the man (it should be pointing up and to the right since the ground is pushing up and to the right). The extra blue and red arrows are unnecessary.

If these are torques , like in a pendulum?, they act tangentially or perpendicularly?
Please , anyone give me the correct values for the three notes ((1),(2),3)) this would help me most.

One of the reasons to simplify the diagram is that it makes calculating the torques much easier. If the system is in static equilibrium then the torque is 0 about any axis. So, to simplify things we can take the axis to be the center of gravity. All three forces pass through the center of gravity so their torque about the center of gravity is 0.

I how do I find the force acting on the pivot, here?

Since the man is in static equilibrium, if you know the tension, T=300, and you know the weight, W=750, then you can use Newton's second law, ∑F=ma with a=0 to find the reaction force, R, at the ground. So $W+T+R=0$ by Newton's second law. If you break that up into components then:

Vertical: $|W| \sin(-90)+|T|\sin(180)+|R|\sin(\theta)=0$
Horizontal: $|W|\cos(-90)+|T|\cos(180)+|R|\cos(\theta)=0$

That gives us two equations in two unknowns* $|R|$ and $\theta$. Solving you get $|R|=808 N$ and $\theta=68°$.

Can you, also, tell me how to use signs, shall I follow the cartesian axes or what?

As long as you are consistent in your convention it does not matter too much, everything will come out correctly. In the above I measured angles counter clockwise from the ground. So $\theta$ is a positive acute angle, gravity is acting at -90° and the tension is acting at 180°.

I could have picked any different convention for my angles, and as long as I used it consistently, I would have obtained the same results.

*note that you gave 45° as a known angle, but that makes the system overdetermined. If you specify the angle then the tension must be an unknown. You can only specify two parameters out of the set {θ, R, W, T}.

 

[CWatters]

I don't understand your diagram. Where does the -750 figure come from?

 

[CWatters]

Since the man is in static equilibrium, if you know the tension, T=300, and you know the weight, W=750...

If the 750 is the mans weight I don't think he can be in equilibrium.

The torques don't appear to sum to zero...

300*1*sin(45) + (-750)*1*cos(45) ≠ 0

PS: This is now the one leg problem isn't it? There is no rear leg to support part of his weight or have I misunderstood post #12 ?

 

[Dale]

If the 750 is the mans weight I don't think he can be in equilibrium.

The torques don't appear to sum to zero...

300*1*sin(45) + (-750)*1*cos(45) ≠ 0

PS: This is now the one leg problem isn't it? There is no rear leg to support part of his weight or have I misunderstood post #12 ?

Yes, this is the one-leg problem. bobie accidentally overspecified the problem, I assumed that the weight and the tension were known and the angle and ground reaction were unknown. Also, as drawn the torques are guaranteed to sum to 0, regardless of the angle and the reaction force since all three pass through the center of gravity.

 

[bobie]

Yes, this is the one-leg problem. bobie accidentally overspecified the problem, I assumed that the weight and the tension were known and the angle and ground reaction were unknown. Also, as drawn the torques are guaranteed to sum to 0, regardless of the angle and the reaction force since all three pass through the center of gravity.

Yes I considered the real weight of a man 75 kg.
I have put the right values for equilibrium.

T300

I am glad that we reached a first important conclusion. I added what is most important for me the x force on the foot :300N

Now this shows what I was not able to express clearly: that the force on the rope -300 cannot by itself for a force on the pivot of 424, which generates a counter force from the block of 300N,
The extra 124 must come from (300N) gravity .Therefore if we add the rear leg this must carry only 450N and the man system will be in equilibrium.
I hope I didn't get it wrong again. If that is right, can I add the rear leg? The problem is: where , at what distance /angle from CM must the rear foot be in order to carry 400N not 1N more not 1 less in order to be in equilibrium? I suppose the normal from CM must fall outside (behind) the foot in order to carry only 40Kg and exercise a net force of 300 on CM, but have no clue about which formula to use.

Thanks Dalespam, you know me, please tell me when you run out of patience!

 

[Dale]

I am glad that we reached a first important conclusion. I added what is most important for me the x force on the foot :300N

Now this shows what I was not able to express clearly: that the force on the rope -300 cannot by itself for a force on the pivot of 424, which generates a counter force from the block of 300N,
The extra 124 must come from (300N) gravity

I don't know where you got these numbers. The force at the ground is 808 N at 68°. The x component is indeed 808 cos(68) = 300 N and the y component is 808 sin(68) = 750 N. I don't know where 424 or 124 come from.

I showed you how to get the correct answer from Newton's 2nd law. Did you understand that? If not, please ask specific questions.

 

[bobie]

Is this what you meant?
If the forces were equal 300 and 300 we would have equilibrium, and applying the parallelogram I would find the force on the pivot = 424.

I returned to the case of equilibrium G = 300.
Specific question: the last image is fundamental, I 'll never change it if you confirm it's OK, now we need to know where to put the rear leg so that it carries exactly 450N, so that 300N go to compensate the pull.I supposed it must be on the left of the CM, so that the normal falls outside the body, is that right?

question: what is the formula to calculate the distribution of the weight on two legs? In which position of the rear leg /if gravity is 750 N) the system is again in equilibrium?

Thanks, consider that the lasr question.

 

[Dale]

I returned to the case of equilibrium G = 300.

I don't know what you mean by "returned to the case of equilibrium". Everything I did assumed equilibrium, so we never left the case of equilibrium. How are we returning to it when we never left it.

Equilibrium is defined by ∑f=0 and ∑τ=0. I solved for ∑f=0 above, as shown, and because all of the forces go through the same point ∑τ=0 is guaranteed.

If G is the weight then it seems like you are changing the weight from 750 N to 300 N, which is fine, but it would help if you would not just randomly change things. With a weight of 300 N then the force at the ground is 424 N at an angle of 45°. Is that what you had intended?

 

[sophiecentaur]

I don't know what you mean by "returned to the case of equilibrium". Everything I did assumed equilibrium, so we never left the case of equilibrium. How are we returning to it when we never left it.

Equilibrium is defined by ∑f=0 and ∑τ=0. I solved for ∑f=0 above, as shown, and because all of the forces go through the same point ∑τ=0 is guaranteed.

If G is the weight then it seems like you are changing the weight from 750 N to 300 N, which is fine, but it would help if you would not just randomly change things. With a weight of 300 N then the force at the ground is 424 N at an angle of 45°. Is that what you had intended?

Yes. I was a bit surprised by a reference to Newton 2, earlier on. There need be only vanishingly small acceleration. To get the 'just enough' condition- so you start to get motion, you just have to replace the Equation with an Inequality - giving the same numerical answer.

 

[CWatters]

Specific question: the last image is fundamental, I 'll never change it if you confirm it's OK.

I believe this the "last image"..

http://s47.photobucket.com/user/lis...[user]=141333040&filters[recent]=1&sort=1&o=0

This does not appear to be consistent.

The man cannot lean at 45 degrees and only produce a force of 300N.

Dale assumed that you had made a mistake on the diagram and in his post #127 he calculated the angle had to be 68 degrees.

Q: Do you agree with his calculation?

If not then why not?

It's not acceptable to keep changing the problem when you don't agree with the solution given for the previous version.

 

[CWatters]

question: what is the formula to calculate the distribution of the weight on two legs? In which position of the rear leg /if gravity is 750 N) the system is again in equilibrium?

I refer you to the basic procedure I outlined in post #107

I know you didn't like the assumptions I made (rear leg under COM) but the basic procedure is the same. Just modify it to suit your new version of the problem.

 

[bobie]

I refer you to the basic procedure I outlined in post #107
.

I have made a sketch of both the situation in equilibrium
http://s47.photobucket.com/user/lisa0rg/media/Double_zps8dcf5a18.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0

The Fx (friction?) on the foot remains 300, should we conclude that whenever there is equilibrium, whatever the angle and whatever weight, it will always be 300? that is amazing.

I made also a sketch of the distribution of weight on each leg, and it seems that Friction is always the same (and opposite) at each foot, the weight here is 800N
http://s47.photobucket.com/user/lisa0rg/media/ManAstr_zps15a9bd01.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=1
Can you please answer these simple specific questions:

- what is called friction when the foot is not slipping but is firm against an obstacle.
- shall I call the friction that prevents the truck from moving stiction?
- the 300N required to move the truck are working only against stiction, since non-zero energy is required to move it is friction is 0

I hope I made it, at last.

Thanks, you have been really kind

 

[A.T.]

- what is called friction when the foot is not slipping but is firm against an obstacle.

The contact force component parallel to the contact surface is stiction (static friction).

- shall I call the friction that prevents the truck from moving stiction?

It's rather complex. Stiction in the bearings, rolling resistance due to deformation of tires.

- the 300N required to move the truck are working only against stiction, since non-zero energy is required to move it is friction is 0

When stiction breaks down, kinetic friction appears.

 

[bobie]

The contact force component parallel to the contact surface is stiction (static friction).
It's rather complex. Stiction in the bearings, rolling resistance due to deformation of tires.
When stiction breaks down, kinetic friction appears.

So 300N are necessary to overcome to stiction and rolling resistance. What is kinetic friction? does any of the force go into KE at all?
Are all three sketches all right, at last?

 

[A.T.]

What is kinetic friction?

http://en.wikipedia.org/wiki/Friction#Kinetic_friction

But when you think about bearings, they actually use rolling, so it's more rolling resistance due to deformation, rather than kinetic friction.

does any of the force go into KE at all?

When the truck accelerates at v>0, yes.

 

[bobie]

http://en.wikipedia.org/wiki/Friction#Kinetic_friction
When the truck accelerates at v>0, yes.

If memory serves, in another thread wasnt't it you or as it another who maintained that if there is no friction I can move anything with 'negligible' energy?

 

[A.T.]

If memory serves, in another thread wasnt't it you or as it another who maintained that if there is no friction I can move anything with 'negligible' energy?

If there is no friction (or other resistance), moving something at constant speed doesn't require any energy input.

 

[CWatters]

The Fx (friction?) on the foot remains 300, should we conclude that whenever there is equilibrium, whatever the angle and whatever weight, it will always be 300? that is amazing.

As stated, in horizontal equilibrium the horizontal components sum to zero. The only two horizontal components are the 300N force at the rope and friction. So these must be equal and opposite. If they aren't the same then there would be a net horizontal force on the man and he wouldn't be in equilibrium.

I made also a sketch of the distribution of weight on each leg, and it seems that Friction is always the same (and opposite) at each foot...

For the same reason as above. If they were different there would be a net horizontal force on the man and he would start accelerating! Clearly that cannot happen if the only horizontal forces are due to friction (Friction can't be a source of energy).

 

[A.T.]

Friction can't be a source of energy.

Friction with a static object can't be a source of energy. In a reference frame where the ground moves, friction with the ground can do positive work.

 

[jbriggs444]

Friction with a static object can't be a source of energy. In a reference frame where the ground moves, friction with the ground can do positive work.

The above is certainly correct.

If one examines the sum of the work done by each object on the other in a pair that are interacting only with friction then the total [center-of-mass] work done across the interface can only be zero or negative.

I think that this is the sense of "can't be a source of energy" that CWatters had in mind.

 

[Dale]

http://s47.photobucket.com/user/lisa0rg/media/Double_zps8dcf5a18.jpg.html?filters[user]=141333040&filters[recent]=1&sort=1&o=0

These seem fine to me. What they show is that a one legged child (weighing 300 N) has to lean back much further than a one legged man (weighing 750 N) if they each want to exert 300 N tension in the rope. That makes sense and goes along with what you would intuitively expect.

The only potential suggestion I would make is to somehow indicate that the 300 N horizontal force (black arrow) is a component of the ground reaction force (green arrow) and not a separate force. Usually, when I was doing free-body diagrams for homework, I would indicate that by placing the back of both arrows at the same point and making a dotted line from the tip of one arrow to the tip of the other arrow (forming a little triangle with the two vectors). That is not essential, as long as it is understood, but just a suggestion to keep in the back of your mind for future free-body diagrams.

The Fx (friction?) on the foot remains 300, should we conclude that whenever there is equilibrium, whatever the angle and whatever weight, it will always be 300? that is amazing.

That is guaranteed by the equilibrium condition that ∑f=0. It is not a general rule of nature, but an assumption of the problem.

 

[bobie]

Usually, when I was doing free-body diagrams for homework, I would indicate that by placing the back of both arrows at the same point and making a dotted line from the t.

You mean something like this:
"Force of inertia" is not a commonly used term. Furthermore, it is unclear if there is some physics concept you are actually asking

If you think some sketch are useful for future viewers, please attach them to relative posts, as I am going do delete my account at bucketshop, and I do not know how to do it. When I clik 'image' they give me no choice to apload from my PC.

 

[Dale]

You mean something like this

No, I mean on the drawing, indicating that one arrow is not a separate force, but just an identified component of another force by something like this.

 

[bobie]

No, I mean on the drawing, indicating that one arrow is not a separate force, but just an identified component of another force by something like this.

I posted wrong link , I mean something like this (this is the final sketch)
http://s47.photobucket.com/user/lis...[user]=141333040&filters[recent]=1&sort=1&o=0