Forces proportional to the sides of a quadrilateral result in a couple

[gnits]

Homework Statement

To prove forces around a quadrilateral form a couple

Relevant Equations

Balance of linear forces and torques

Can I please ask for help with the following:

Forces proportional to the sides of a quadrilateral taken in order act respectively along those sides. Prove that the resultant of the system is a couple whose magnitude is represented by twice the area of the quadrilateral.

Not sure where to start here. To be a couple I need to show that the resultant is pure torque. So I might start by showing that the horizontal and vertical resultant is zero. Here's a diagram, but it isn't helping me much (does this question hold true if the quadrilateral is concave?):

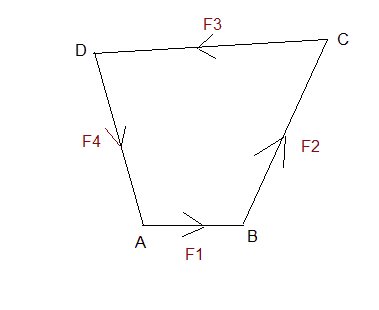
(could define x-axis to run A to B and y-axis to be vertical).

Let:

|AB| = a
|BC| = b
|CD| = c
|DA| = d

Then, is the question saying:

F1 = k * a
F2 = k * b
F3 = k * c
F4 = k * d
(For a scalar k).

If so I don't see how to go about showing that the horizontal and vertical resultant will be zero.

Thanks for any help,
Mitch.

 

[Master1022]

Hi,

Not sure where to start here. To be a couple I need to show that the resultant is pure torque. So I might start by showing that the horizontal and vertical resultant is zero. Here's a diagram, but it isn't helping me much (does this question hold true if the quadrilateral is concave?):

View attachment 269941

What if you think of this as a force polygon? I think that will immediately help you prove the sum of the forces is 0. Remember when adding force vectors, we can connect up the vectors from head to toe to get the net result... For example, if you start at A and connect the force vectors up, where do you end up? What is the length of that vector?

Spoiler: Spoiler

The net force is 0

I hope that made some sense. If not, do let me know and I will try to explain further.

For the proof that there is a net torque, I don't exactly have a rigorous proof (I am sure another helper might be able to provide a better insight there). However, we can rely on the fact that the vector moment of a couple is the same about any point.

[EDIT]: The remainder of this post only helps to show that the system does reduce to a couple, but does not (to my knowledge) help prove that the magnitude of the couple is twice the area. Perhaps once you have proven the first two things and make some progress, you can show work towards the final part for contributors to look over.

Given that we don't have numerical values and the fact that you can take moments about any point (even outside the quadrilateral), you might want to see whether you can find a point such that it is geometrically visible that there will indeed be a net moment. I hope that provides a starting place and I have included a hint below.

[EDIT #2]: apologies about all the edits (just had more ideas come to mind). There are alternative choices of points on the quadrilateral that can be chosen to take moments about which will show that the system reduces to a couple.

Spoiler: Hint # 1

What happens if you were to extend any two sides of the quadrilateral and look at where they intersect? What if you took moments about that point?

Spoiler: Hint # 2

What happens if you were to extend any AD and BC and take moments about the point of intersection

 

[Steve4Physics]

Hi. Master1022 has explained why the resultant is zero. For the couple (total moment), draw the 2 diagonals: can you use their point of intersection?

 

[gnits]

Thank you both for your help. You enabled me to see how to understand and solve the question. It really puzzled me at first. Indeed it is essential that the magnitudes of the forces be proportional to the lengths of the sides so that one can legitimately form the force polygon. That was the subtlety which I had not seen. Taking moments about the intersection of the diagonals then helped me to see that the torque was not zero.

Thanks to both of you.

 

[Steve4Physics]

Hi. Did you also relate the couple to the area? Using the 2 the diagonals splits the quadrilateral into 4 triangles. Each force is the base of a triangle. The area-couple relationship is then simple (but ask if you can't see it).

 

[gnits]

Sorry, yes forgot to mention that the help I received also let me solve this part.

Thanks,
Mitch.