Formula to use instead of model

In summary, the conversation discusses a study where 5 test subjects are brought in each month and administered 1 monthly test for 3 months. The speaker is looking for a formula or technique to calculate the number of expected tests per month and the total number of tests for a larger number of subjects and varying study lengths. However, it is suggested that manually counting the number of subjects enrolled each month would be the most efficient method.
  • #1
BTH
2
0
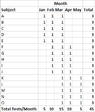
Scenario: An average of 5 test subjects are brought into a study in subsequent months and are administered 1 monthly test for as long as they remain part of the study. The time they remain in the study is 3 months.

Could someone please explain a formula or technique to sum the number of expected tests per month and total if possible in lieu of having to model it out like below to capture the dynamic of subjects rolling on and off over time? My real example has many more subjects and time on study varies, so a formula would save a lot of time at scale.

View attachment 7679
 

Attachments

  • Test cascade.PNG
    Test cascade.PNG
    3 KB · Views: 91
Mathematics news on Phys.org
  • #2
I don't think there's anything that's going to make this more convenient than counting the number of users enrolled during a particular month. Using a spreadsheet will speed things up somewhat.
 

FAQ: Formula to use instead of model

1. What is a formula?

A formula is a mathematical expression that describes a relationship between variables. It is often used to make predictions or solve problems in a specific field of study.

2. How is a formula different from a model?

A formula is a specific mathematical expression that can be used to make calculations, while a model is a more general representation of a system or phenomenon. A model can incorporate multiple formulas and other factors to provide a more comprehensive understanding.

3. When should a formula be used instead of a model?

A formula should be used instead of a model when the problem at hand is well-defined and can be solved using a specific set of equations. Models are often used when the problem is more complex and requires a more comprehensive approach.

4. Are there limitations to using a formula instead of a model?

Yes, there are limitations to using a formula instead of a model. Formulas are only applicable in specific situations and may not account for all variables and factors that may affect the outcome. Models, on the other hand, can incorporate a wider range of variables and provide a more accurate representation of the problem.

5. Can a formula be used in all scientific fields?

No, formulas are specific to the field of study in which they were developed. Different scientific fields have their own unique formulas that are used to solve problems within that particular field. However, some formulas may have applications in multiple fields if the problem being solved is similar.

Similar threads

MHB How to Model Capacity for Training 5000 Trainees Annually?
Replies
1
Views
2K
MHB Demand and Regression Analysis
Replies
4
Views
3K
I Exploring the Galactic Center: Adaptive Optics & GR
Replies
1
Views
932
A Modeling the damping of a physical rigid pendulum
Replies
1
Views
857
I Simple lateral vehicle dynamics model
Replies
18
Views
2K
A "The 7 Strangest Coincidences in the Laws of Nature" (S. Hossenfelder)
2
Replies
62
Views
5K
A Why is there no distance-measure in the standard model?
Replies
6
Views
2K
Looking for equation/formula for calculating boomerang trajectory based on few variables for game
Replies
0
Views
1K
Radical new cosmic model (Barrau Linsefors one-up Penrose)
Replies
8
Views
5K
Should I study D. S. Processing or control theory in greater depth?
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top