Morbert said:
1. Unless explicitly stated otherwise, all my descriptions below are in accordance with Mjelva's projection-based account.
2. The evolution only acts on 2 & 3. In the case we are considering, where Alice and Bob recorded VV...
so no matter what Victor does the run belongs to the set where 1 & 4 are VV. This cannot be undone even though 2 & 3 are subject to change. So a BSM result by Victor both i) subjects 2&3 to change and ii) belongs to the set of runs where Alice & Bob recorded HH or VV (assuming they measured in the H/V basis).
3. Here is what happens if Alice and Bob record LL: The state collapses to $$ \begin{eqnarray*}\ket{LL}_{14}\ket{RR}_{23} & =& \ket{LL}_{14}\otimes(\ket{H}_2 + i\ket{V}_2)\otimes(\ket{H}_3 + i\ket{V}_3)/2\\
&=&\ket{LL}_{14}\otimes(\ket{HH}_{23}-\ket{VV}_{23} +i\ket{HV}_{23}+i\ket{VH}_{23})/2\\
&=&\ket{LL}_{14}\otimes(\ket{\phi^-}_{23} +i\ket{\psi^+}_{23})/\sqrt{2}\end{eqnarray*}$$If Victor performs an SSM on this state, he can get any of the four possible results for 2 & 3. If Victor attempts a BSM, he can only get either Φ- or fail. No matter what Victor does, this run is one where Alice and Bob measured LL. 1 & 4 don't change.
4. If Alice and Bob record LR respectively, then we have the projection onto ...
5. You can see that, for all cases above, no true swap occurs.
6. When Alice and Bob complete their measurements, 1 & 4 are projected onto a separable state that does not change no matter what Victor does. All Victor can do is keep or discard each run based on a measurement he might or might not do: A measurement that has no effect on 1 & 4.
1. Great. Also
@Morbert (and everyone else!): Thanks for the time and effort put in to follow these interesting related papers, and the detail of the theory and experiment. I know it gets difficult to follow at times. I can't speak for anyone else, but I am gaining a lot of understanding just working through the various permutations.
2. That's the Morbert/Mjelva hypothesis. Agreed otherwise.
3. Fully agreed as to your first equation line, I consider this canonical. The second and third lines are incorrect, unless they are supposed to be
post-swap. After all, before the swap, they have no connection whatsoever and there is nothing to connect these particular photons. So I'll assume
post-swap is what you intend, and continue on that line.
So... I agree that if we go SSM (no swap), any of the 4 outcomes are possible. And I agree that we evolve after a BSM (swap) to what you have for equation lines 2 & 3 post swap, where we are agreeing that there
is a physical change. So if Alice and Bob see LL: Victor can see |Φ->
23 outcomes but not |Φ+>
23 outcomes. I'm
not agreeing that this evolution actually occurs as you present it; but I will take this idea forward and see where it leads. We will see shortly that it is contradicted by basic entanglement theory.
4. Agreed conditionally as per 3.
5. This is inconsistent with your statement that there is evolution to entangled Bell states when a swap occurs. Obviously, this is a physical change. The first line of your 3./4. scenarios NEVER evolves to the second line unless a physical action occurs: namely, there is physical overlap in the Beam Splitter.
6. It would seem you have presented an argument supporting your hypothesis in point 2, although you must acknowledge what I said in point 5. But... don't celebrate quite yet!
There is a major theoretical problem with your premise that once 1 & 4 are measured as LL, they can evolve to a Φ- (or from LR to Φ+).
This is physically impossible, and only can occur when full 4-fold analysis is done.
Specifically: A peculiarity of Type II parametric down conversion (PDC) sources, as used in the Ma experiment, is that they require tight restrictions on output cones.
They must overlap to create polarization entangled pairs. You could alternately select from conic sections that are labeled Vertical and Horizontal, as marked in the diagram below. In that case, the output pairs will have known polarizations |VH>. They will NOT be polarization entangled. Such unentangled pairs can be manipulated (with suitable wave plates) as desired to be any of |HV>
12, |LR>
12 or |+->
12. Let's call this variation "Ma-X" if it were to be hypothetically executed in the same Ma setup we have been discussing.
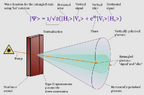 Ma-X
Ma-X: If the sources of the pairs are intentionally made to be |LR>
12 and |RL>
34 (i.e. not in the Ψ- Bell state per the actual experiment), then Alice and Bob will observe |LL>
14 - exactly per your 3. Also, as you state, the middle pair is |RR>
23. And that means that if a BSM occurs, that evolves exactly as you say so that the middle pair is now in the entangled state (|Φ->
23 + |Ψ+>)
23/√2. You are saying "no true swap occurs".
In the Ma-X scenario: there is no correlation between the |LL>
14 outcomes and the |Φ->
23 outcomes versus the |Φ+>
23 outcomes. That is basic entanglement swapping theory, you must have the source pairs entangled for the BSM to lead to a physical swap across 4 photons. And yet, if your concept of the evolution of the state of the 2 & 3 photons were correct, there should be the same results as Ma observed in the Figure 3a (L/R basis).
In other words: for all Ma-X results, there will be an approximately equal number of |Φ-> BSMs and |Φ+> BSMs. But you say that |Φ+> BSMs
only belong with |LR>
14 or |RL>
14 results by Alice and Bob.
In the quantum world:
Entanglement Swapping is manifested by a 4-fold context that spans both space and time. Given the usual predictions of QM, it is not possible to provide a meaningful
forward in time only description, as either you or Mjelva sought to do here. Of course, there are Interpretations that might get around this issue with other assumptions. IMHO: They would still need to consider a 4-fold context.
Edited to add:
-For polarization, Ma tests 3 mutually unbiased bases: H/V, +/- (usually +45 degrees/-45 degrees), and L/R. The general rules apply identically regardless of which of these are being discussed, and generally the basis can be changed from one to the other by appropriate use of wave plates.
-How do we know I'm right about the Ma-X outcomes being different than the original Ma experimental setup? Well, obviously they wouldn't need to overlap Vertical/Horizontal cone regions if that wasn't a requirement (see diagram) to obtain successful entanglement swapping.
-I would characterize the relationship between photons 2 & 3 - after a BSM - as entangled, regardless of whether a swap occurs with photons 1 & 4. In the Ma-X scenario, that is what occurs. That entanglement is essentially useless though.
