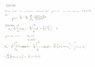SUMMARY
The discussion revolves around solving a Fourier Series representation problem, specifically focusing on calculating the coefficients \( a_n \). The participant, Andrew, struggles with the integration process and seeks guidance on handling the integral correctly. Another user points out an error in Andrew's integration by parts, noting that he dropped the variable \( n \) in the argument of the integral. This feedback confirms that Andrew's approach is fundamentally sound, allowing him to proceed with his solution.
PREREQUISITES
- Understanding of Fourier Series and their applications
- Knowledge of integration techniques, specifically integration by parts
- Familiarity with handling mathematical notation in discussions
- Basic proficiency in calculus, particularly with infinite series
NEXT STEPS
- Review the process of calculating Fourier coefficients, particularly \( a_n \)
- Study integration by parts in detail, focusing on common pitfalls
- Explore examples of Fourier Series problems and their solutions
- Learn about the convergence of Fourier Series and its implications
USEFUL FOR
Students studying advanced calculus, particularly those tackling Fourier Series problems, as well as educators looking for common student misconceptions in integration techniques.