BobP
- 70
- 1
I have been very briefly introduced to Fourier transformations but the topic was not explained especially well (or I just didn't understand it!)
We were shown the graphs with equations below and then their Fourier transformation (RHS). I understand the one for cos(2pist) but NOT the sin(2pist).
Here is my reasoning: The sin wave shown has a constant frequency (that is larger than the cosine function; hence its frequency values are larger). It is possible to have a "-ve" frequency because waves can travel in both directions. I do not understand why the amplitude on the sin graph is negative though? If it was negative on both it would make sense but it isn't!
I know that both FT boil down to a cosine expression (as the sin expression is lost when integrating between infinities) and that makes it even more confusing for me! Please can someone help me understand. thanks
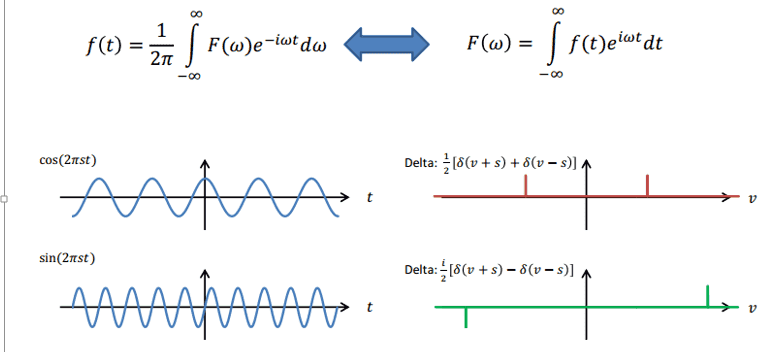
We were shown the graphs with equations below and then their Fourier transformation (RHS). I understand the one for cos(2pist) but NOT the sin(2pist).
Here is my reasoning: The sin wave shown has a constant frequency (that is larger than the cosine function; hence its frequency values are larger). It is possible to have a "-ve" frequency because waves can travel in both directions. I do not understand why the amplitude on the sin graph is negative though? If it was negative on both it would make sense but it isn't!
I know that both FT boil down to a cosine expression (as the sin expression is lost when integrating between infinities) and that makes it even more confusing for me! Please can someone help me understand. thanks