- #1
MexChemE
- 237
- 55
Hello, PF!
I am currently learning Fourier series (and then we'll move on to the Fourier transform) in one of my courses, and I'm having a hard time finding motivation for its uses. Or, in other words, I can't seem to find its usefulness yet. I know one of its uses is to solve the heat equation, which is why we're learning Fourier series in the first place, but aside from that, other applications are not so evident. Now, I'm not trying to disregard Fourier series as a useful mathematical tool, I'm actually really interested in mastering this technique and the Fourier transform, I just need help in order to see the whole picture.
For example: most textbooks, when presenting the technique, state that it is a useful tool for expressing a periodic function as a sum of sines and/or cosines, and should only be used on periodic functions. What is the point of this, if the function is already, by definition, periodic?
Then, one of my exercises asks to find the Fourier sine series of [itex]f(x) = 1 - x[/itex] for the interval [itex][0,\pi][/itex], which is
[tex]f(x) = \frac{2}{\pi} \sum_{n=1}^{\infty} \frac{1-(-1)^n+\pi(-1)^n}{n} \ \sin{nx}[/tex]
I plotted the results in order to see what is actually going on.
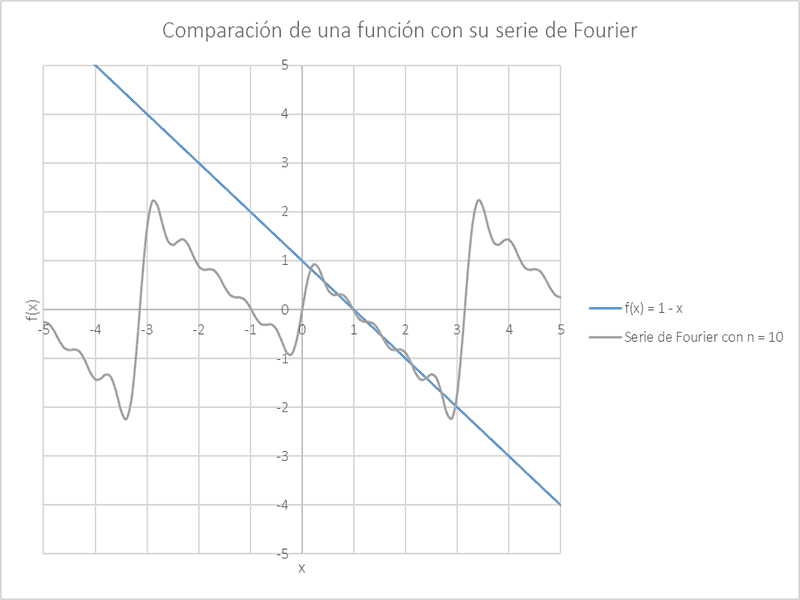
As you can see, the series approximate the function the most between 0 and [itex]\pi[/itex] (roughly). It seems obvious that the series will approximate the function only for the given interval, is this the rule? Now, regarding this same example, what would be the point of having a function like this and obtain its Fourier series, application-wise? What can you do with it?
Regarding the Fourier transform, what I understand is that you can use it to obtain a series for a function, but for the entire real domain, that is [itex](-\infty,\infty)[/itex]. However, this impression might be wrong, as it also changes the independent variable, which doesn't happen when you obtain the Fourier series of the function. Speaking of which; I understand that when your independent variable is time, the Fourier transform takes you into the frequency domain. But, what happens when the independent variable is x, as in position? What is the physical meaning of the variable change?
Thanks in advance for any input, I tried to be as clear as possible, which I hope I did!
I am currently learning Fourier series (and then we'll move on to the Fourier transform) in one of my courses, and I'm having a hard time finding motivation for its uses. Or, in other words, I can't seem to find its usefulness yet. I know one of its uses is to solve the heat equation, which is why we're learning Fourier series in the first place, but aside from that, other applications are not so evident. Now, I'm not trying to disregard Fourier series as a useful mathematical tool, I'm actually really interested in mastering this technique and the Fourier transform, I just need help in order to see the whole picture.
For example: most textbooks, when presenting the technique, state that it is a useful tool for expressing a periodic function as a sum of sines and/or cosines, and should only be used on periodic functions. What is the point of this, if the function is already, by definition, periodic?
Then, one of my exercises asks to find the Fourier sine series of [itex]f(x) = 1 - x[/itex] for the interval [itex][0,\pi][/itex], which is
[tex]f(x) = \frac{2}{\pi} \sum_{n=1}^{\infty} \frac{1-(-1)^n+\pi(-1)^n}{n} \ \sin{nx}[/tex]
I plotted the results in order to see what is actually going on.
As you can see, the series approximate the function the most between 0 and [itex]\pi[/itex] (roughly). It seems obvious that the series will approximate the function only for the given interval, is this the rule? Now, regarding this same example, what would be the point of having a function like this and obtain its Fourier series, application-wise? What can you do with it?
Regarding the Fourier transform, what I understand is that you can use it to obtain a series for a function, but for the entire real domain, that is [itex](-\infty,\infty)[/itex]. However, this impression might be wrong, as it also changes the independent variable, which doesn't happen when you obtain the Fourier series of the function. Speaking of which; I understand that when your independent variable is time, the Fourier transform takes you into the frequency domain. But, what happens when the independent variable is x, as in position? What is the physical meaning of the variable change?
Thanks in advance for any input, I tried to be as clear as possible, which I hope I did!