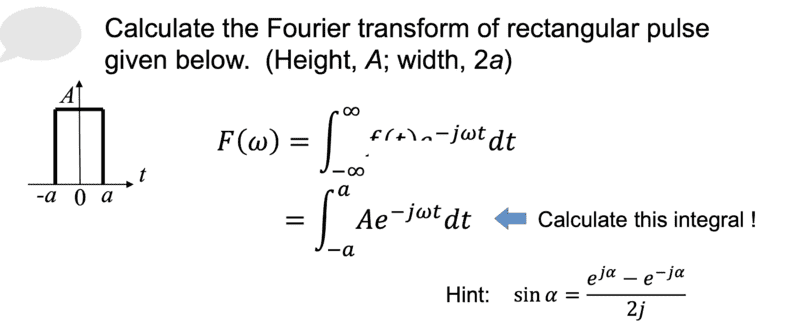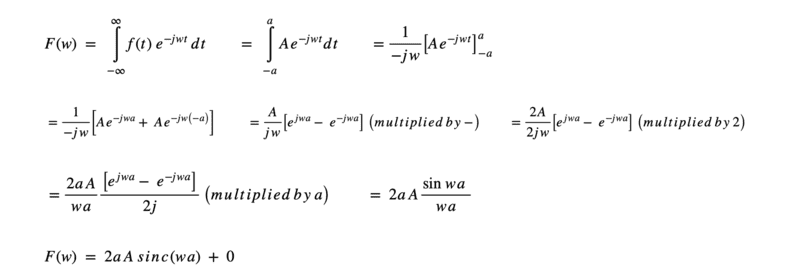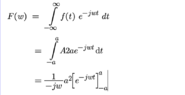Discussion Overview
The discussion revolves around the Fourier transform of a rectangular pulse, specifically addressing the application of the width of the pulse in calculations and the implications of changing this width. Participants explore the relationship between the time and frequency domains, as well as the mathematical expressions involved in the Fourier transform process.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants confirm that the final result of the Fourier transform is correct, while others express confusion about the application of the width (2a) in calculations.
- There is a discussion about how the width of the pulse in the time domain (2a) relates to the frequency domain, where it appears to have infinite width.
- Participants debate the necessity of including 2a in the calculations and how it affects the mathematical expressions, particularly in relation to the sinc function.
- Some participants suggest that the width appears through the bounds of integration and is essential for the final result, while others question the utility of including it in certain calculations.
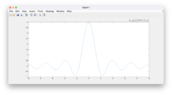
- There is a discussion about the implications of changing the width of the rectangular pulse on the shape of the magnitude spectrum and the behavior of the sinc function.
- Participants also discuss the use of software like Matlab for visualizing the results of the Fourier transform and express uncertainty about the conversion of calculations into graphical representations.
Areas of Agreement / Disagreement
Participants generally express differing views on the application of the width (2a) in calculations, with no consensus reached on its necessity in all contexts. While some agree on the behavior of the Fourier transform with respect to changes in width, the discussion remains unresolved regarding the specific mathematical treatment of 2a.
Contextual Notes
Limitations include the dependence on definitions of width in both time and frequency domains, and the unresolved nature of how to incorporate 2a into calculations without altering the function being transformed.