- #1
mickonk
- 7
- 0
Hi. I'm familiar with Fourier series but I have some hard times in learning Fourier transform. Why we use it? What's purpose of Fourier transform? Here is one signal and plot of Fourier transform of that signal:
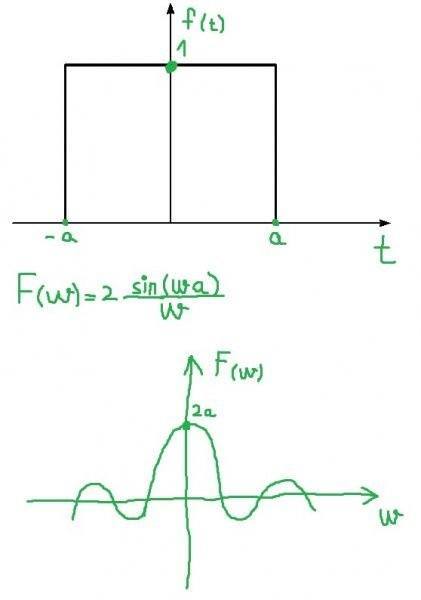
What this graph tells us? Thanks in advance.
What this graph tells us? Thanks in advance.