Free Body Diagrams: Easily Analysing Photos & Sketches

[lazypast]

Hi,

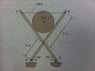
When looking at a photo or sketch, I find it hard to take out the important bits and turn it into a freebody diagram. I am doing this question (pic attached).

Im quite unsure how to even begin. I've though of a few ways to start analysing it.

The first way analyses AD as a whole. And essentially all the forces would produce a moment about C.

the bottom pic shows the forces (the ball exerts 800N) and I would calculate the reactions in the supports. I would be tempted to find the reactions then put them back into the analysis mentioned above (moments about C). The only prob is, I am not sure its as easy as saying ƩF(y)=0. ∴Reaction(D) = Reaction(E) = -400N.

Are there any pointers? I do have the solutions manual however Id just like a nudge in the right direction before taking a peek. Thanks.

 

[PhanthomJay]

When you look as the system as a whole, yes, the reactions at E and D must be vertical upward and equal, at 400 N each, assuming the ball weighs 800 N (does it?). You can sum moments about E = 0 to find the upward reaction at D, and then use your sum of forces = 0 in y direction to find the upward reaction at E, to get this result. You should also sum forces in the x direction to solve for any horizontal force at E, if there is one (is there?).
Then when you try to find the other forces at joints A, B, and C, you can break apart one of the members as you have done (but show it as a diagonal as it it exists, don't flatten it out), and sum moments about C to get B, etc. However, if the ball weighs 800 N, the vertical force from the sphere is not 800 N in this FBD..what should it be?

 

[lazypast]

Thanks for the guidance.
I see the reactions are 400N = R(e) = R(d) and there are no horizontal reactions. What I have been doing is resolving parallel and perpendicular to the plane.

I will try your method of taking moments about C. I would love to see a mathmatical way of finding out the distance between C and the point of contact of the ball and member. I've forgotton too much maths to do it myself, so I employed some CAD help (pic attached).

The distance is 0.86m, so now I will resolve the forces perpendicular to the member and take moments about C, i.e.

(1)400cos55 + (0.86)800cos55 = (2)F_{AB}sin55

Rearranging F_{AB} = 230+395/(2sin55) = 381N

This is not the answer in the back of the book, I must be missing somthing.

 

[PhanthomJay]

Thanks for the guidance.
I see the reactions are 400N = R(e) = R(d) and there are no horizontal reactions.

Good.

What I have been doing is resolving parallel and perpendicular to the plane.

OK

I will try your method of taking moments about C. I would love to see a mathmatical way of finding out the distance between C and the point of contact of the ball and member. I've forgotton too much maths to do it myself, so I employed some CAD help (pic attached).

The distance is 0.86m,

you're a lot better at CAD than I, so I'll take your word that 0.86 m is correct, since I'm also pretty bad at geometry

so now I will resolve the forces perpendicular to the member and take moments about C, i.e.

(1)400cos55 + (0.86)800cos55 = (2)F_{AB}sin55

Almost correct, but not quite...that middle term (0.86)800cos55 is incorrect...its that 800 number that is wrong...part of the ball's weight is on the other member...so that 800 number should instead be ___?___. Otherwise, this is real good.

 

[lazypast]

Thanks for the guidance. I now have the answer. Due to symmetry and resolving vertically I arrived at 800=2Rcos55 where R is the perpendicular force exerted on 1 member and equals 697N.

Although it's now solved I am still curious about 1 thing, C. We can either take moments again or sum the perpendicular forces and see there is a force at C of about 53N. Futhermore summing parallel forces to the member, we get a parallel component of C at about 37N. The resultant is 65N at an angle 36degrees from the vertical (Pointing down).

When I started to analyse this system I assumed I would have to know about C. Could anyone provide detail on point C. The forces seem minimal compared to the outermost points of the member, is that because the moment is far smaller? When analysing systems like this in industry, is point C never a point of particular interest? (i.e. we're interested in the outermost points).

Once again thanks

 

[PhanthomJay]

Thanks for the guidance. I now have the answer. Due to symmetry and resolving vertically I arrived at 800=2Rcos55 where R is the perpendicular force exerted on 1 member and equals 697N.

Although it's now solved I am still curious about 1 thing, C. We can either take moments again or sum the perpendicular forces and see there is a force at C of about 53N. Futhermore summing parallel forces to the member, we get a parallel component of C at about 37N. The resultant is 65N at an angle 36degrees from the vertical (Pointing down).

I think you should find that the resultant at C is horizontal.

When I started to analyse this system I assumed I would have to know about C. Could anyone provide detail on point C. The forces seem minimal compared to the outermost points of the member, is that because the moment is far smaller? When analysing systems like this in industry, is point C never a point of particular interest? (i.e. we're interested in the outermost points).

Once again thanks

Connection design at C is governed by the forces at C.

 

[lazypast]

I've been picking things apart. There is 1 question: Why is there no parallel component at the point of contact between the ball and the member? There are parallel forces at all other points on the member.

If there were a parallel force, the resultant at C is not horizontal! But I would guess there is a parallel force because if one member were to disappear the ball would accelerate down the slope of the other member.

I can only assume since we look at the whole picture, we can see the horizontal reactions at C and B balances the horizontal component at the ball contact (i.e. the resultant at the ball contact is 697N and the vertical is 400N, so the horizontal ≈570N.)

If the vertical is 400N, surely the parallel at the ball contact is 400cos35 = 328N.

Thanks

 

[PhanthomJay]

I've been picking things apart. There is 1 question: Why is there no parallel component at the point of contact between the ball and the member?

Any parallel force at that point would have to be from friction, but the ball would rest there just fine even if the member was frictionless. There is only a Normal force there perp. to the member, with a mag. of 697 N, and with vert. comp. of 400 N and horiz. comp. of 570 N.

If there were a parallel force, the resultant at C is not horizontal! But I would guess there is a parallel force because if one member were to disappear the ball would accelerate down the slope of the other member.

there is none.

I can only assume since we look at the whole picture, we can see the horizontal reactions at C and B balances the horizontal component at the ball contact (i.e. the resultant at the ball contact is 697N and the vertical is 400N, so the horizontal ≈570N.)

yes

If the vertical is 400N, surely the parallel at the ball contact is 400cos35 = 328N.

Thanks

The parallel comp. of the 400 N vert. force plus the parallel comp. of the 570 N horiz. force must sum to 0...thus, there is no parallel force.
Bottom line is that the force at C is 65 N in a horizontal direction.