SUMMARY
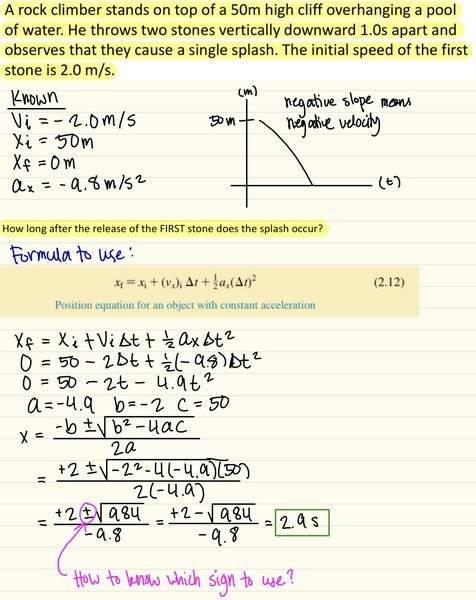
The quadratic equation was utilized to determine the time of free fall, yielding a solution of 3 seconds. The discussion highlighted the importance of selecting the correct sign when solving for time, emphasizing that the negative solution corresponds to a physical constraint where time must be positive. The incorrect use of the positive sign resulted in a non-viable solution of 3.4 seconds. The key takeaway is that when applying the quadratic formula, one must consider the context of the problem to select the appropriate root.
PREREQUISITES
- Understanding of the quadratic formula
- Familiarity with parabolic functions
- Basic knowledge of physical constraints in motion problems
- Ability to interpret mathematical solutions in real-world contexts
NEXT STEPS
- Study the application of the quadratic formula in physics problems
- Learn about the significance of physical constraints in mathematical solutions
- Explore examples of parabolic motion and their graphical representations
- Review common mistakes in solving quadratic equations and how to avoid them
USEFUL FOR
Students studying physics, mathematics educators, and anyone seeking to understand the application of quadratic equations in real-world scenarios.