Friction and Energy Conservation in Ball Colliding with Wall

[Saitama]

Homework Statement

Homework Equations

The Attempt at a Solution

I have dealt with the case when the wall is frictionless and the rolling ball collide with it but I am not sure how to proceed here. When the ball comes in contact with the wall, the friction due to wall acts in the vertically upward direction for a very short time. Hence,
$$\int fR\,dt=I(\omega_f-\omega_i)$$
and
$$\int f\,dt=mv_i$$
where $f$ is the friction due to wall and $R$ is the radius of ball. How do I relate $v_i$, $\omega_f$ and $\omega_i$? (where $v_i$ is the velocity acquired by ball in vertically upward direction.)

Also, which angle does the problem talks about? Is it the angle made by line joining the intersection of wall and floor with centre of ball and the ground?

Any help is appreciated. Thanks!

 

[collinsmark]

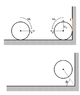
Hello Pranav-Arora,

You always get the best physics problems!

Homework Statement

Homework Equations

The Attempt at a Solution

I have dealt with the case when the wall is frictionless and the rolling ball collide with it but I am not sure how to proceed here. When the ball comes in contact with the wall, the friction due to wall acts in the vertically upward direction for a very short time. Hence,
$$\int fR\,dt=I(\omega_f-\omega_i)$$

That's the right idea. But I want you to be careful of the signs. Is the torque on the left hand side of the equation (represented by fR) in the same direction as the ω terms? In other words, is it going to act to speed up the rotation or slow it down?

and
$$\int f\,dt=mv_i$$
where $f$ is the friction due to wall and $R$ is the radius of ball. How do I relate $v_i$, $\omega_f$ and $\omega_i$? (where $v_i$ is the velocity acquired by ball in vertically upward direction.)

I used different variable names. I used $v_{iy}$ = 0 as the initial velocity in the y-direction and $v_{fy}$ as the final in the y-direction. But that's neither here nor there. You can use whichever variable names you want.

The key to the relationship is to note that the ball does not slip against the wall when it touches the wall.

In other words, for an instant, after the impact, the ball sort of rolls up the wall. Not with the same velocity of v, but some different velocity, $v_i$ (what I called $v_{fy}$), for which you will solve.

The ball doesn't really roll against the wall because it has a component in the x-direction. But if we ignore the x-direction for the moment, and focus only on the y-direction, the ball rolls against the wall (immediately after the impact). That should give you a relationship between $v_i$ (what I called $v_{fy}$) and $\omega_f$.

Also, the magnitude of the impulse vector (in vector form, $\vec J = \int \vec f(t)dt$) can be treated as a constant. $J = \int f(t)dt$. No integration is necessary. Just substitute in a $J$ and leave it at that.

Also, which angle does the problem talks about? Is it the angle made by line joining the intersection of wall and floor with centre of ball and the ground?

Any help is appreciated. Thanks!

I interpret that as an acute angle with the floor. For example, if the ball simply rolls back on the floor (which it won't), the angle is 0^o. If it goes straight up against the wall (which it won't) the angle is 90^o.

 

[Saitama]

Hi collinsmark!

You always get the best physics problems!

Thanks!

That's the right idea. But I want you to be careful of the signs. Is the torque on the left hand side of the equation (represented by fR) in the same direction as the ω terms? In other words, is it going to act to speed up the rotation or slow it down?

I knew I was messing up with the signs, let me clear everything. Please have a look at the attachment. I consider anticlockwise sense to be positive and I follow your notation for the final vertical velocity.

$$\int fR\,dt=I(\omega_f+\omega_i)\,\,\,\, (*)$$
(plus sign because $\omega_i$ is clockwise)
$$\int f\,dt=mv_{fy}\,\,\,\, (**)$$

I used different variable names. I used $v_{iy}$ = 0 as the initial velocity in the y-direction and $v_{fy}$ as the final in the y-direction. But that's neither here nor there. You can use whichever variable names you want.

The key to the relationship is to note that the ball does not slip against the wall when it touches the wall.

From the non-slipping condition, I have
$$\omega_i=\frac{v}{R}$$
$$\omega_f=\frac{v_{fy}}{R}$$
From the above relations, (*) and (**), I get:
$$mv_{fy}R=I\left(\frac{v_{fy}}{R}+\frac{v}{R}\right)$$
Also, $I=(2/5)mR^2$. Plugging this and solving for $v_{fy}$, I get
$$v_{fy}=\frac{2v}{3}$$
The maximum height attained by the ball is given by:
$$h=\frac{v_{fy}^2}{2g}=\frac{4v^2}{18g}$$
The position of the ball from the wall when this maximum height is attained is:
$$x=\frac{4v^2}{3g}$$

I interpret that as an acute angle with the floor. For example, if the ball simply rolls back on the floor (which it won't), the angle is 0^o. If it goes straight up against the wall (which it won't) the angle is 90^o.

Does the question asks angle $\theta$ shown in attachment? If so, then
$$\tan\theta=\frac{h}{x}=\frac{1}{6}$$
$$\Rightarrow \theta=9.462^{\circ}$$

 

[voko]

I knew I was messing up with the signs, let me clear everything. Please have a look at the attachment. I consider anticlockwise sense to be positive and I follow your notation for the final vertical velocity.

$$\int fR\,dt=I(\omega_f+\omega_i)\,\,\,\, (*)$$
(plus sign because $\omega_i$ is clockwise)
$$\int f\,dt=mv_{fy}\,\,\,\, (**)$$

I do not think this and the picture are correct. In the picture, you have the ball rolling backward after the collision. How do you justify that? If we assume that it is still in contact with the wall at this stage, it must also be rolling downward. This cannot be true.

I think you should assume that the direction of rotation is preserved (clockwise), but the angular speed is changed.

But what you do have to take into account is the direction of torque (counter-clockwise).

The maximum height attained by the ball is given by:
$$h=\frac{v_{fy}^2}{2g}=\frac{4v^2}{18g}$$
The position of the ball from the wall when this maximum height is attained is:
$$x=\frac{4v^2}{3g}$$


Does the question asks angle $\theta$ shown in attachment? If so, then
$$\tan\theta=\frac{h}{x}=\frac{1}{6}$$
$$\Rightarrow \theta=9.462^{\circ}$$

That would be true if the motion was in a straight line, which it is not. What is the direction of the velocity after the collision?

 

[collinsmark]

I knew I was messing up with the signs, let me clear everything. Please have a look at the attachment. I consider anticlockwise sense to be positive and I follow your notation for the final vertical velocity.

I've redrawn parts of the diagram with my own take on it.

I'm pretty sure that there is no mechanism that could bring the ball to rotate in the opposite direction in this situation. The ball is rotating clockwise before it hits the wall, and it is still rotating clockwise after it leaves the wall -- it's not rotating as fast! The rotation has slowed down a bit -- but it is still rotating clockwise.

Friction against the wall is the only force acting on the ball. So unless the wall itself is moving (like a vertical conveyer-belt), there's nothing that could cause the ball to change its direction of rotation such that the ball also maintains an upward, linear velocity.

Remember, the ball is glued against the wall for that short time of impact. If the ball is moving up a little (which it is), it must maintain its clockwise rotation. Otherwise it would imply slipping, or some other force involved.

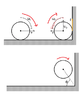
Here is my take of the diagram.

I've tried to indicate the the angular rotation has slowed down a little by the smaller arrow after it hits the wall. But it is still moving clockwise.

Which is related to another point that I mentioned in my last post about the torque.

The ball's rotation is clockwise, but the what direction is the torque? I believe the torque would be in the anticlockwise direction. That would make ω_f smaller than ω_i, not larger.

$$\int fR\,dt=I(\omega_f+\omega_i)\,\,\,\, (*)$$
(plus sign because $\omega_i$ is clockwise)

Changing the plus sign to a minus sign wasn't what I was referring to in my last post. You are looking for the change in angular momentum (which is what R times the impulse is). So there still needs to be a subtraction involving ω_f and ω_i.

In your last post you had,

$$ \int f R \ dt = I(\omega_f - \omega_i) $$

But from what I can tell from that equation (directly above), the torque would cause the ball to speed up its rotation.

I think you need to either switch your ω_f and ω_i around, or put a negative sign on the ∫fRdt.

Something to account for the torque being in the opposite direction of the rotation. The final angular velocity will end up being smaller than the initial angular velocity.

$$\int f\,dt=mv_{fy}\,\,\,\, (**)$$

That one looks fine though. The force is in the up direction and the final momentum is in the up direction. All looks good to me there.

From the non-slipping condition, I have
$$\omega_i=\frac{v}{R}$$
$$\omega_f=\frac{v_{fy}}{R}$$
From the above relations, (*) and (**), I get:
$$mv_{fy}R=I\left(\frac{v_{fy}}{R}+\frac{v}{R}\right)$$
Also, $I=(2/5)mR^2$. Plugging this and solving for $v_{fy}$, I get
$$v_{fy}=\frac{2v}{3}$$
The maximum height attained by the ball is given by:
$$h=\frac{v_{fy}^2}{2g}=\frac{4v^2}{18g}$$
The position of the ball from the wall when this maximum height is attained is:
$$x=\frac{4v^2}{3g}$$

I didn't see anything in the original problem statement about finding the maximum height.

The way I understood the problem, it only asks for the angle immediately after the impact.

If so, the answer should be the same angle for any ball, anywhere. I don't think gravity, the size of the ball, the speed of the ball play a role in the final answer.

Does the question asks angle $\theta$ shown in attachment? If so, then
$$\tan\theta=\frac{h}{x}=\frac{1}{6}$$
$$\Rightarrow \theta=9.462^{\circ}$$

I got a different answer for my angle and vertical velocity, but that's just because of the torque direction vs. rotation direction I mentioned above.

 

[Saitama]

In the picture, you have the ball rolling backward after the collision. How do you justify that?

If I showed the ball at a height above the ground, would it be correct then?

If we assume that it is still in contact with the wall at this stage, it must also be rolling downward. This cannot be true.

Rolling downward?

I think you should assume that the direction of rotation is preserved (clockwise), but the angular speed is changed.

Yes, the direction should stay preserved as it would slip if the direction was counter-clockwise.

I make the equations again:
$$\int fR\,dt=I(-\omega_f+\omega_i)$$
$$\int f\,dt=mv_{fy}$$
Hence, $v_{fy}=(2/7)v$.

Is it correct now?

That would be true if the motion was in a straight line, which it is not. What is the direction of the velocity after the collision?

I never said that the motion is straight line. Probably my image isn't accurate enough. Sorry.

The motion is like a projectile.

 

[collinsmark]

I make the equations again:
$$\int fR\,dt=I(-\omega_f+\omega_i)$$
$$\int f\,dt=mv_{fy}$$
Hence, $v_{fy}=(2/7)v$.

Is it correct now?

That's what I got.

Now just use your inverse tangent method to find the angle and we're all set!

 

[voko]

If I showed the ball at a height above the ground, would it be correct then?

Rolling downward?

Yes, if the direction of the rotation becomes counter-clockwise while still in contact with the wall, it will be rolling downward.

Yes, the direction should stay preserved as it would slip if the direction was counter-clockwise.

I make the equations again:
$$\int fR\,dt=I(-\omega_f+\omega_i)$$
$$\int f\,dt=mv_{fy}$$
Hence, $v_{fy}=(2/7)v$.

Is it correct now?

It seems so.

I never said that the motion is straight line. Probably my image isn't accurate enough. Sorry.

The motion is like a projectile.

Yes, but I do not see that you finding the direction of its velocity correctly. The angle that you found is not the angle of the velocity with the ground.

 

[Saitama]

Now just use your inverse tangent method to find the angle and we're all set!

I tried finding the angle between the final horizontal and vertical velocity vectors and it seems to work but I don't get why this is the answer. It doesn't make sense.

 

[voko]

I agree that the wording of "make an angle with the ground" is confusing. Yet the only angle we can really talk about here is the angle of the velocity with the ground. Maximum height is a height, not an angle.

 

[Saitama]

Maximum height is a height, not an angle.

Yes but I found the horizontal position from the wall too because I interpreted it as the angle $\theta$ shown in my sketch where the ball is at maximum height.

Thanks a lot collinsmark and voko!

 

[collinsmark]

I tried finding the angle between the final horizontal and vertical velocity vectors and it seems to work but I don't get why this is the answer. It doesn't make sense.

I agree that the wording of "make an angle with the ground" is confusing. Yet the only angle we can really talk about here is the angle of the velocity with the ground. Maximum height is a height, not an angle.

I really don't think the problem is asking for anything to do with maximum height.

I interpret it as asking for the ball's trajectory immediately after it leaves the wall/floor corner.

I think "angle with the ground" means "angle with respect to the horizontal." I think the configuration you used in your diagram (regarding the angle) is the right idea.

[Edit: By that I mean your $\mathrm{arctan}\left( \frac{v_{fy}}{v} \right)$ is your final answer.]

 

[voko]

[Edit: By that I mean your $\mathrm{arctan}\left( \frac{v_{fy}}{v} \right)$ is your final answer.]

Wait. Why do you assume the horizontal velocity remains unchanged?

 

[collinsmark]

Wait. Why do you assume the horizontal velocity remains unchanged?

It specifically says so in the original problem statement. (Well, opposite direction, but equal magnitude.)

 

[voko]

It specifically says so in the original problem statement. (Well, opposite direction, but equal magnitude.)

Hmm. Why did they want to insist on non-conversation of energy?

 

[collinsmark]

Hmm. Why did they want to insist on non-conversation of energy?

[STRIKE]Now that you mention it, after doing some calculations, not only is energy not conversed, but something seems to have violated the second law of thermodynamics.

Yes, something is definitely wrong with some assumptions with this problem, one way or the other. [/STRIKE]

[Edit: nevermind]

 

[voko]

Second law of thermodynamics? In what way?

 

[collinsmark]

Second law of thermodynamics? In what way?

Sorry. Miscalculation when I was summing up all the energies. I thought for a moment that the ball ended up with more energy than it started with.

One second comparison, it doesn't. So the answer doesn't violate any fundamental physical laws at least. Whew!