Friction problem involving spool

[issacnewton]

Here's the problem statement

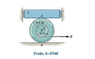
Block C has a mass of 50 kg and is confined between two walls by smooth rollers. If the block rests on top of the 40 kg spool, determine the minimum cable force P needed to move the spool. The cable is wrapped around the spool's inner core . The coefficients of static friction at A and B are \mu_{A}=0.3 and \mu_{B}=0.6.

The problem is Problem 8-48 from "Engineering Mechanics-Statics, R.C.Hibbeler 12th edition"
Now here's my attempt at solution. As P increases, there will develop force,say f₁
at A, which will act in the same direction as P to oppose the torque created by P. Also there will develop a force f₂ at B in the direction opposite to that of P, again to oppose the torque by P. Now when the spool is about to move (impending motion), f₁ and f₂ will have values of their respective maximum static friction values. Since spool is still not rotating or translating, we can use two conditions of stability, viz, net force on the spool is zero and net torque on the spool is zero. We can setup the following equations.

P+f_1=f_2 and

0.2P=0.4f_1+0.4f_2

but this leads to strange condition that f_1=-\frac{P}{4} which means that
f₁ and P are in opposite direction. How can that be ? Am I missing to take some information into account ?

Thanks

 

[tiny-tim]

hi IssacNewton!

(have a mu: µ )

As P increases, there will develop force,say f₁
at A, which will act in the same direction as P to oppose the torque created by P.

hmm … if the block wasn't there, how much would the https://www.physicsforums.com/library.php?do=view_item&itemid=39" force f₂ at B be?

and so which way would the spool turn? ​

(if you've nothing better to do this weekend, try this:

if the engine drives only the front wheels of a car, in which direction is the friction force on the front and on the back wheels? )

 

[zorro]

I think the direction of f1 in translational motion equation is wrong.
f1 and f2 are static frictional forces which always act to oppose the relative motion between two bodies. So here f1 and f2 both will be in a direction opposite to P.
I got P as 705.6N. Is it right?

 

[issacnewton]

hmm … if the block wasn't there, how much would the friction force f₂ at B be?

and so which way would the spool turn? ​

(if you've nothing better to do this weekend, try this:

if the engine drives only the front wheels of a car, in which direction is the friction force on the front and on the back wheels? )

Hi tiny-tim, I think friction force f₂ would still point opposite to the P. right ?

about your week end quiz, I just found an awesome material on the web today on the topic
of rolling motion. Check this.

http://cnx.org/content/m14384/latest

http://cnx.org/content/m14385/latest

check other modules on this website.

http://cnx.org/content/search?words=rolling&allterms=weakAND&search=Search

most of the modules on rolling motion are written by a guy named Sunil Kumar Singh and they are very good. so much information on rolling motion is not covered on intro books like halliday, serway. I am glad I found these links.

To answer your question, if its an accelerated pure rolling motion (so no deformation at the contact surface , which means no rolling resistance), then axle will exert a torque on the
front wheel, which will cause the static frictional force to act in the forward direction at the contact surface. but the force will be exerted at the center of mass at the back wheel in the forward direction ,so the static friction will act in the direction opposite to the motion of the car since the line of action of this force passes through the center of mass of the back wheel. The links I have posted above, talk EXACTLY this stuff

So I hope that my answer is correct.

 

[issacnewton]

I think the direction of f1 in translational motion equation is wrong.
f1 and f2 are static frictional forces which always act to oppose the relative motion between two bodies. So here f1 and f2 both will be in a direction opposite to P.
I got P as 705.6N. Is it right?

Hi, I don't know the answer. I have PDF of this book and they have given answers to only some problems. But can you show how you got the answer ?

 

[zorro]

Hi, I don't know the answer. I have PDF of this book and they have given answers to only some problems. But can you show how you got the answer ?

Lol. The admin will send me an infraction if I show you how I got the answer.
I just changed the direction of f1.
P = f1 + f2
and used the torque equation accordingly.

 

[tiny-tim]

hi IssacNewton!

about your week end quiz, I just found an awesome material on the web today on the topic
of rolling motion. Check this.
http://cnx.org/content/m14384/latest"
http://cnx.org/content/m14385/latest"

(whyever did you put them in quote boxes? )

i'm sorry, i don't like the reasoning about the direction of friction in that second link

in particular, Sunil Kumar Singh's conclusion (about the line of action of the force) is simply wrong …

Summary

4: Direction of friction :

(i) If the force passes through center of mass, then there is sliding tendency in the forward direction of applied force. In turn, friction acts in backward direction of the external force.

(ii) If the force does not pass through center of mass, then it constitutes torque. There is sliding tendency due to torque in the backward direction of applied force. The net result is that there is either no net friction (in special circumstance) or there is friction in the forward direction.

… so if the force passes just a nanometre away from the centre of mass, suddenly the direction of friction is reversed??

no, Sunil Kumar Singh has taken some standard cases and overgeneralised from them

his method usually gives the right result, but that doesn't make it right

the correct test is: what would happen if there was no friction (for example, if one surface was ice)?

in your original question, that's fairly easy to see, but sometimes it's really difficult, in which case i prefer to change to a frame of reference moving (and maybe accelerating) with the centre of mass …

in other words: pretend you're on a seat attached to the centre of mass (but remaining upright! ), and looking down at the wheel …

because you're (pretending to be) stationary, that means that the wheel is also stationary, but rotating, and that the other surface is moving in the "backward" direction …

if the other surface was ice, would the applied forces make the bottom of the wheel move backward faster than the road is moving backward? if yes, the friction on the wheel is forward; if no, the friction is backward ​

for example, if a car's engine is accelerating, and if a non-driving tyre (only) is on ice, that tyre will rotate at the same speed (because there are no turning forces on it), but the car will go faster (because there is an external force from the driving tyres that aren't on ice): looking down from the window, you see the road going backward faster than the tyre is going backward, so the road will try to drag the tyre backward with it

in other words: the tendency is for the road to move backward relative to a non-driving tyre, so the friction on the road is forward, and the friction on the tyre is backward

but if the driving tyres (only) are on ice, those tyres will rotate faster (because the engine is directly turning them, and accelerating … the lack of friction on the ice doesn't matter), but the car will stay the same speed (because there are no external forces on it): looking down from the window, you see the road going backward slower than the tyres are going backward, so the road will try to drag the tyres forward with it

in other words: the tendency is for the road to move forward relative to the driving tyres, so the friction on the road is backward, and the friction on the tyres is forward!

suppose, finally, that the car is four-wheel drive, but that one pair of tyres is receiving less power from the engine than the other pair …

Sunil Kumar Singh's test (about the line of action of the force) give the wrong result! ​

anyway, to return to the plot …

Hi tiny-tim, I think friction force f₂ would still point opposite to the P. right ?

yeees, but what i asked was " if the block wasn't there, how much would the friction force f₂ at B be?"

… and so, if the block wasn't there (or was ice), which way would the spool turn?

 

[issacnewton]

well may be you are right about those modules. this topic is very frustrating though. physics textbooks like serway, halliday don't cover such detail about the rolling motion and even in "engineering mechanics-Statics, R.C.Hibbeler 12th edition" (I have PDF of this) the author doesn't go into so much detail as this Sunil Singh has done. If you find any books or websites discussing this topic thoroughly , let me know.

coming to the problem I posted, if the block wasn't there then the spool will accelerate to the left. we can set the following equations of motion

f_2-P=ma_{cm} for translational motion

and \tau_{net}=0.2P-0.4f_2=I\alpha

now that author, Sunil Singh, says in his notes that for the rolling motion we have the condition that

a_{cm}=-\alpha R

I didn't understand the minus sign, but let's assume it here. so with this we can eliminate
a_{cm} from both the equations. and we get

f_2=\frac{I-0.08m}{I-0.16m}\, P

so where do we go from here ?

 

[tiny-tim]

… if the block wasn't there then the spool will accelerate to the left.

no!

hmm … I've asked twice already, and you still haven't answered …

if the block wasn't there, how much would the friction force f₂ at B be?

why are you ignoring these hints?

then, using that value for f₂, which way would the spool turn? and so which way would the spool roll?

btw, you've been assuming …

… Now when the spool is about to move (impending motion), f₁ and f₂ will have values of their respective maximum static friction values.

that's not so … one of them will reach the maximum value first, and then the spool will slide along that surface, but will roll along the other surface

 

[issacnewton]

tiny-tim, I have actually given the value of f_2 in terms of P. so I have given
the answer to your question about "How much"

 

[tiny-tim]

(just got up :zzz: …)

tiny-tim, I have actually given the value of f_2 in terms of P. so I have given
the answer to your question about "How much"

you mean … ?

coming to the problem I posted, if the block wasn't there then the spool will accelerate to the left. we can set the following equations of motion

f_2-P=ma_{cm} for translational motion
…

no, we're just testing which way the spool "wants" to go, not trying to solve the whole thing …

we put a = 0 and get f₂ = P …

ok, if f₂ = P (and if the block wasn't there), which way would the spool turn? and so which way would the spool roll?

 

[issacnewton]

Ok, so if the spool doesn't move to the left, the only way it can move is to the right

but why ?

 

[tiny-tim]

Ok, so if the spool doesn't move to the left, the only way it can move is to the right

but why ?

why is the sky blue? why is heat hot?

it just does!

you can tell from the torque equation (equations don't lie! ), or …

you can even tell from the constraint equation (conservation of length of the string) … mark a point on the string, see how far round the spool it goes, and you'll find, as a matter of geometry not of forces, that the hand moves half as fast in the same direction as the spool does