- #1
HighPhy
- 89
- 8
- Homework Statement
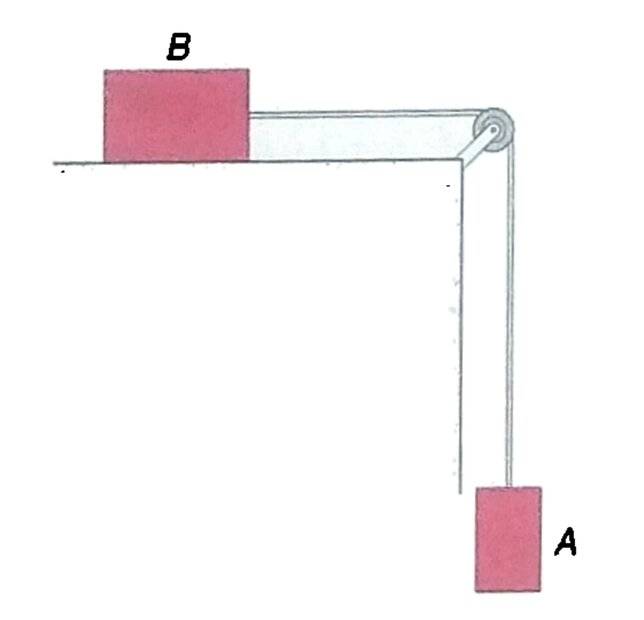
- Consider two bodies ##A## and ##B## connected as in the figure below. The horizontal surface where B is laid is rough with static friction coefficient ##\mu_s = 0.4## and kinetic friction coefficient ##\mu_k = 0.35##. The mass of B is ##m_B = 4 \ \mathrm{kg}##, the wire that connects ##A## and ##B## is an elastic of negligible mass and elastic constant ##k = 160 \ \mathrm{N/m}##; initially the system is at rest because ##A## is supported with an external force and the elastic has a length equal to that at rest. At instant ##t = 0##, the force ##m_A\boldsymbol{g}## that holds ##A## in equilibrium is eliminated.
##a)## What is the maximum value ##m^{\ast}## that the mass of ##A## can have if ##B## is to remain stationary?
##b)## If ##m_A = 3m^{\ast}##, with which acceleration does ##A## leave and at what instant, and with which acceleration does ##B## leave?
- Relevant Equations
- Too many to summarize. See "Attempt at a Solution".
(This is a homework assignment that my sister (younger than me) didn't manage to solve, but I am not sure about the attempt I thought of either. Especially in the last point. So I ask you to correct where I am wrong).
I solved ##a)## with the following:
1. Since ##B## must be stationary, I derived the maximum elongation of the spring from the equation of harmonic motion of ##A## (solution of a non-homogeneous ODE);
2.I imposed equilibrium on mass ##B## using the above elongation and then equated the corresponding elastic force to the static friction force between mass ##B## and the supporting plane. The relationship between ##m^{\ast}## and ##m_B## is thus obtained;
I am developing these two points.
1. Suppose we let the mass down gently so it comes to rest at the equilibrium length of the spring.
This equilibrium length is given by ##ky_0 = mg##, so: ##y_0 = \frac{m_Ag}{k}##.
Now we'll define a new variable ##z## as ##z = y - y_0##, so using this new variable the equilibrium position of the mass is ##z = 0##.
And then the EoM using the variable ##z## is:
$$\frac{\mathrm{d}^2z}{\mathrm{d}t^2} = -\frac{k}{m_A}z \ .$$
Suppose we displace the mass a distance $z$ from the equilibrium position, then the net force on the mass is $$F = kz \ .$$
And if we solve this equation we get:
$$z(t) = A \sin(\omega t) + B \cos(\omega t) \ ,$$
where ##\omega^2 = \dfrac{k}{m} \ .##
Now we know that at time ##t = 0## we have ##z = -y_0## and ##\frac{\mathrm{d}z}{\mathrm{d}t} = 0 \ .##
And if we substitute these values of ##z## and ##t## into our equation we find ##A = 0## and ##B = -y_0 \ .##
So our equation is:
$$z(t) = -y_0 \cos(\omega t) \ .$$
And we defined our variable ##z## as:
$$z = y - y_0 \ .$$
So now we can substitute for ##z## to get:
$$y - y_0 = -y_0 \cos(\omega t) \ .$$
And rearranging gives:
$$y = y_0 - y_0 \cos(\omega t)$$
or:
$$y = y_0(1 - \cos(\omega t)) \ .$$
Ultimately:
\begin{equation}
y = \frac{m_Ag}{k}\left(1 - \cos (\omega t) \right)
\end{equation}
Deriving with respect to time, we obtain the velocity:
$$\dot{y} = \frac{m_Ag}{k} \omega \sin (\omega t) \ ,$$
which is zero at ##\omega t= \pi \quad (1.1)##, instant at which the elongation (and thus the restoring force) is maximum. So:
$$\dot{y} = 0 \iff \omega t= \pi$$
Plugging ##(1.1)## in ##(1)##:
$$y_{\mathrm{max}} = \frac{m_Ag}{k}\left(1 - \cos (\pi) \right) = \frac{2m_A g}{k}$$
2. For balance of forces:
$$F_{\mathrm{friction}} = F_{\mathrm{elastic}} \implies F_{\mathrm{friction}} = \cancel{k} \frac{2m_A g}{\bcancel{k}} = 2 m_A g \ .$$
Using the fundamental inequality of friction ##F_{\mathrm{friction}} \leq F_{\mathrm{friction, \ max}} = \mu_s m_B g##:
$$2 m_A g \leq \mu_s m_B g \Rightarrow m_A \leq \frac{\mu_s}{2} m_B \ ,$$
from which
$$\color{Red}{\boxed{\color{Black}{m_{A, \ \mathrm{max}} = m^{\ast} = \frac{\mu_s}{2} m_B = 0.8 \ \mathrm{kg}}}}$$
##b)## I obtained the acceleration with which mass ##A## departs by deriving the EoM ##(1)## twice and setting ##t = 0##.
$$\color{blue}{\mathrm{First \ step)}} \ \color{Black}{\ddot{y} = \frac{mg}{k} \omega^2 \cos(\omega t) \stackrel{\omega^2 = k/m}{\boldsymbol{=\!=\!=\!=}} \frac{\cancel{m}}{\bcancel{k}} g \frac{\cancel{k}}{\bcancel{m}} \cos(\omega t) = g \cos(\omega t)}$$
$$\color{blue}{\mathrm{Second \ step)}}
\ \color{Black}{\ddot{y} = g \cos(\omega t) \stackrel{t = 0}{\boldsymbol{=\!=\!\Rightarrow}}\ddot{y} = g \cos 0} \Rightarrow \color{Red}{\boxed{\color{Black}{\ddot{y} = g}}}$$
I then obtained after how long ##B## starts by substituting the elongation of the wire that starts ##B## found previously (i.e. the one that wins the force of static friction) in the EoM of mass ##A## .
Mass ##B## leaves when ##F_{\mathrm{friction}} = F_{\mathrm{friction, \ max}} = \mu_s m_B g##. From balance of forces:
$$F_{\mathrm{friction}} = F_{\mathrm{elastic}} \implies \mu_s m_B g = k \delta \ ,$$
where ##\delta## is the elongation of mass ##B##.
From that:
$$\delta = \frac{\mu_s m_B g}{k} \ ,$$
and plugging it in ##(1)## by placing ##\delta = y##, I got:
\begin{align*}
\frac{\mu_s m_B g}{k} = \frac{m_Ag}{k}\left(1 - \cos (\omega t) \right)
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
\left(1 - \cos (\omega t)\right) = \mu_s \frac{m_B}{m_A}
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
\cos (\omega t) = \left(1 - \mu_s \frac{m_B}{m_A}\right)
\end{align*}
\begin{align*}
\Bigg{\Downarrow} \ \omega = \sqrt{\frac{k}{m_A}}
\end{align*}
\begin{align*}
\sqrt{\frac{k}{m_A}} t = \arccos{\left(1 - \mu_s \frac{m_B}{m_A}\right)}
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
t = \sqrt{\frac{m_A}{k}} \arccos{\left(1 - \mu_s \frac{m_B}{m_A}\right)}
\end{align*}
\begin{align*}
\Bigg{\Downarrow} \ m_A = 3 m^{\ast} = \frac{3}{2} \mu_s m_B
\end{align*}
\begin{align*}
t = \sqrt{\frac{3}{2} \frac{\mu_s m_B}{k}} \arccos{\left(1 - \cancel{\mu_s} \dfrac{\cancel{m_B}}{\frac{3}{2} \bcancel{\mu_s} \bcancel{m_B}}\right)}
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
\color{Red}{\boxed{\color{Black} {t = \sqrt{\frac{3}{2} \frac{\mu_s m_B}{k}} \arccos \left({\frac{1}{3}}\right) \approx 0.15 \ \mathrm{s}}}}
\end{align*}
I now have to calculate with what acceleration ##B## starts, a point on which I found some conceptual difficulties; in particular, for a while I could not see how to introduce the kinetic friction coefficient (since body ##B## starts from a standstill) and which equations to use.
I made the following rationale:
The static friction for B is ##\mu_s m_B g##, so ##B## starts to move when the tension in the rope is equal to ##\mu_s m_B g##.
At the instant ##B## starts to move, the friction becomes kinetic so it decreases to ##\mu_k m_B g##, but the tension in the string is still ##\mu_s m_B g \ .##
So there is a net force on ##B## given by:
$$F = \mu_s m_B g - \mu_k m_B g = (\mu_s - \mu_k) m_B g \ .$$
Applying Newton's 2nd Law on mass ##B##:
$$F = m_B a \Rightarrow (\mu_s - \mu_k) m_B g = m_B a \ , $$
from which:
$$\color{Red}{\boxed{\color{Black} {a = (\mu_s - \mu_k) g}}}$$
About last point, this is the only physical explanation I could think of. But it is not convincing to me, it seems too forced. Could you provide the best physical explanation that effectively resolves this last point?
I solved ##a)## with the following:
1. Since ##B## must be stationary, I derived the maximum elongation of the spring from the equation of harmonic motion of ##A## (solution of a non-homogeneous ODE);
2.I imposed equilibrium on mass ##B## using the above elongation and then equated the corresponding elastic force to the static friction force between mass ##B## and the supporting plane. The relationship between ##m^{\ast}## and ##m_B## is thus obtained;
I am developing these two points.
1. Suppose we let the mass down gently so it comes to rest at the equilibrium length of the spring.
This equilibrium length is given by ##ky_0 = mg##, so: ##y_0 = \frac{m_Ag}{k}##.
Now we'll define a new variable ##z## as ##z = y - y_0##, so using this new variable the equilibrium position of the mass is ##z = 0##.
And then the EoM using the variable ##z## is:
$$\frac{\mathrm{d}^2z}{\mathrm{d}t^2} = -\frac{k}{m_A}z \ .$$
Suppose we displace the mass a distance $z$ from the equilibrium position, then the net force on the mass is $$F = kz \ .$$
And if we solve this equation we get:
$$z(t) = A \sin(\omega t) + B \cos(\omega t) \ ,$$
where ##\omega^2 = \dfrac{k}{m} \ .##
Now we know that at time ##t = 0## we have ##z = -y_0## and ##\frac{\mathrm{d}z}{\mathrm{d}t} = 0 \ .##
And if we substitute these values of ##z## and ##t## into our equation we find ##A = 0## and ##B = -y_0 \ .##
So our equation is:
$$z(t) = -y_0 \cos(\omega t) \ .$$
And we defined our variable ##z## as:
$$z = y - y_0 \ .$$
So now we can substitute for ##z## to get:
$$y - y_0 = -y_0 \cos(\omega t) \ .$$
And rearranging gives:
$$y = y_0 - y_0 \cos(\omega t)$$
or:
$$y = y_0(1 - \cos(\omega t)) \ .$$
Ultimately:
\begin{equation}
y = \frac{m_Ag}{k}\left(1 - \cos (\omega t) \right)
\end{equation}
Deriving with respect to time, we obtain the velocity:
$$\dot{y} = \frac{m_Ag}{k} \omega \sin (\omega t) \ ,$$
which is zero at ##\omega t= \pi \quad (1.1)##, instant at which the elongation (and thus the restoring force) is maximum. So:
$$\dot{y} = 0 \iff \omega t= \pi$$
Plugging ##(1.1)## in ##(1)##:
$$y_{\mathrm{max}} = \frac{m_Ag}{k}\left(1 - \cos (\pi) \right) = \frac{2m_A g}{k}$$
2. For balance of forces:
$$F_{\mathrm{friction}} = F_{\mathrm{elastic}} \implies F_{\mathrm{friction}} = \cancel{k} \frac{2m_A g}{\bcancel{k}} = 2 m_A g \ .$$
Using the fundamental inequality of friction ##F_{\mathrm{friction}} \leq F_{\mathrm{friction, \ max}} = \mu_s m_B g##:
$$2 m_A g \leq \mu_s m_B g \Rightarrow m_A \leq \frac{\mu_s}{2} m_B \ ,$$
from which
$$\color{Red}{\boxed{\color{Black}{m_{A, \ \mathrm{max}} = m^{\ast} = \frac{\mu_s}{2} m_B = 0.8 \ \mathrm{kg}}}}$$
##b)## I obtained the acceleration with which mass ##A## departs by deriving the EoM ##(1)## twice and setting ##t = 0##.
$$\color{blue}{\mathrm{First \ step)}} \ \color{Black}{\ddot{y} = \frac{mg}{k} \omega^2 \cos(\omega t) \stackrel{\omega^2 = k/m}{\boldsymbol{=\!=\!=\!=}} \frac{\cancel{m}}{\bcancel{k}} g \frac{\cancel{k}}{\bcancel{m}} \cos(\omega t) = g \cos(\omega t)}$$
$$\color{blue}{\mathrm{Second \ step)}}
\ \color{Black}{\ddot{y} = g \cos(\omega t) \stackrel{t = 0}{\boldsymbol{=\!=\!\Rightarrow}}\ddot{y} = g \cos 0} \Rightarrow \color{Red}{\boxed{\color{Black}{\ddot{y} = g}}}$$
I then obtained after how long ##B## starts by substituting the elongation of the wire that starts ##B## found previously (i.e. the one that wins the force of static friction) in the EoM of mass ##A## .
Mass ##B## leaves when ##F_{\mathrm{friction}} = F_{\mathrm{friction, \ max}} = \mu_s m_B g##. From balance of forces:
$$F_{\mathrm{friction}} = F_{\mathrm{elastic}} \implies \mu_s m_B g = k \delta \ ,$$
where ##\delta## is the elongation of mass ##B##.
From that:
$$\delta = \frac{\mu_s m_B g}{k} \ ,$$
and plugging it in ##(1)## by placing ##\delta = y##, I got:
\begin{align*}
\frac{\mu_s m_B g}{k} = \frac{m_Ag}{k}\left(1 - \cos (\omega t) \right)
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
\left(1 - \cos (\omega t)\right) = \mu_s \frac{m_B}{m_A}
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
\cos (\omega t) = \left(1 - \mu_s \frac{m_B}{m_A}\right)
\end{align*}
\begin{align*}
\Bigg{\Downarrow} \ \omega = \sqrt{\frac{k}{m_A}}
\end{align*}
\begin{align*}
\sqrt{\frac{k}{m_A}} t = \arccos{\left(1 - \mu_s \frac{m_B}{m_A}\right)}
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
t = \sqrt{\frac{m_A}{k}} \arccos{\left(1 - \mu_s \frac{m_B}{m_A}\right)}
\end{align*}
\begin{align*}
\Bigg{\Downarrow} \ m_A = 3 m^{\ast} = \frac{3}{2} \mu_s m_B
\end{align*}
\begin{align*}
t = \sqrt{\frac{3}{2} \frac{\mu_s m_B}{k}} \arccos{\left(1 - \cancel{\mu_s} \dfrac{\cancel{m_B}}{\frac{3}{2} \bcancel{\mu_s} \bcancel{m_B}}\right)}
\end{align*}
\begin{align*}
\Downarrow
\end{align*}
\begin{align*}
\color{Red}{\boxed{\color{Black} {t = \sqrt{\frac{3}{2} \frac{\mu_s m_B}{k}} \arccos \left({\frac{1}{3}}\right) \approx 0.15 \ \mathrm{s}}}}
\end{align*}
I now have to calculate with what acceleration ##B## starts, a point on which I found some conceptual difficulties; in particular, for a while I could not see how to introduce the kinetic friction coefficient (since body ##B## starts from a standstill) and which equations to use.
I made the following rationale:
The static friction for B is ##\mu_s m_B g##, so ##B## starts to move when the tension in the rope is equal to ##\mu_s m_B g##.
At the instant ##B## starts to move, the friction becomes kinetic so it decreases to ##\mu_k m_B g##, but the tension in the string is still ##\mu_s m_B g \ .##
So there is a net force on ##B## given by:
$$F = \mu_s m_B g - \mu_k m_B g = (\mu_s - \mu_k) m_B g \ .$$
Applying Newton's 2nd Law on mass ##B##:
$$F = m_B a \Rightarrow (\mu_s - \mu_k) m_B g = m_B a \ , $$
from which:
$$\color{Red}{\boxed{\color{Black} {a = (\mu_s - \mu_k) g}}}$$
About last point, this is the only physical explanation I could think of. But it is not convincing to me, it seems too forced. Could you provide the best physical explanation that effectively resolves this last point?