- #1
charmedbeauty
- 271
- 0
Homework Statement
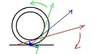
A string is attached to the drum (radius r) of a spool (radius R). (A spool is device for storing string, thread etc.) A tension T is applied to the string at angle θ above the horizontal. The coefficients of kinetic and static friction between floor and spool are μk and μs respectively. We are interested in whether and when the spool will move left or right, and how this depends on the nature of the floor.
Showing all working, calculate the critical value of θ (call it θc) at which the condition goes from rolling to skidding.

Homework Equations
The Attempt at a Solution
ok so I did this...
the point at which its starts skidding is when Nμs=Tcosθc
solving for θc=cos-1(Nμs/T).
but this is wrong I can tell why... because you can't really define an angle by a force... but I don't understand why the expression is wrong,. help please I've been at it for a while. Thanks.
The right answer should be θc=cos-1r/R
but I don't know how they get this?