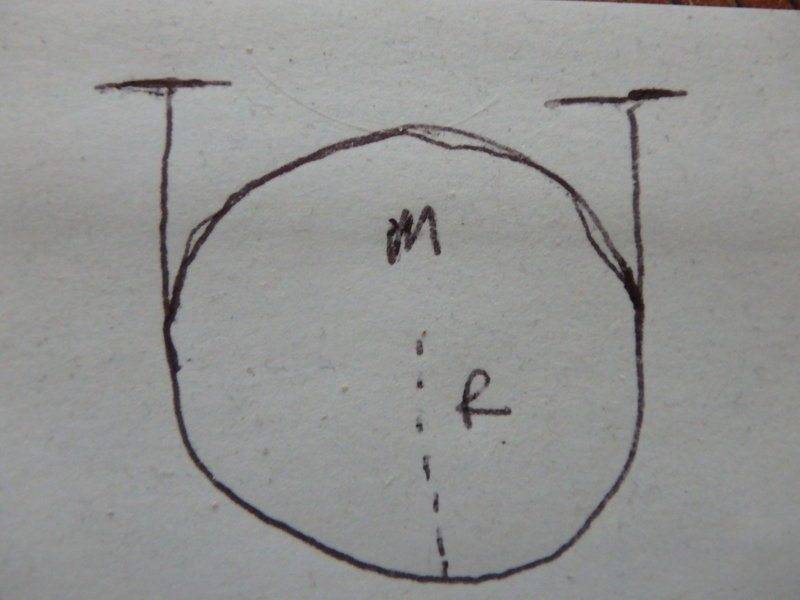
hringsak
In the following diagram, a frictionless disc is supported by a massless string. This problem was given by the author of a book, and a solution was given to some questions that were asked about this diagram. One thing the author said in one of the solutions, was that the tension in the string was equal to Mg/2. Why is this? I would have thought that since the one string is supporting the entire mass of the disc that it should just be Mg.