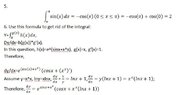SUMMARY
The discussion centers on the application of the Fundamental Theorem of Calculus (FTOC) in solving integral problems. Participants confirm the correctness of solutions to specific questions involving integrals and derivatives. The derivative form of the FTOC is highlighted, stating that if \( G(x) = \int_a^x f(t)\,dt \), then \( G'(x) = f(x) \). The conversation emphasizes the importance of correctly applying the theorem to avoid errors in results, particularly in complex expressions like \( e^{\sin(x) + x^x} \).
PREREQUISITES
- Understanding of the Fundamental Theorem of Calculus
- Knowledge of integral and derivative notation
- Familiarity with exponential functions and their derivatives
- Basic skills in evaluating definite integrals
NEXT STEPS
- Review the Fundamental Theorem of Calculus in detail
- Practice evaluating definite integrals with trigonometric functions
- Explore the properties of exponential functions and their derivatives
- Learn advanced techniques for solving complex integrals
USEFUL FOR
Students studying calculus, educators teaching integral calculus, and anyone looking to deepen their understanding of the Fundamental Theorem of Calculus and its applications.