Galois Groups .... A&F Example 47.7 .... ....

[Math Amateur]

I am reading Anderson and Feil - A First Course in Abstract Algebra.

I am currently focused on Ch. 47: Galois Groups... ...

I need some help with an aspect of the Example 47.7 ...

Example 47.7 and its proof read as follows:

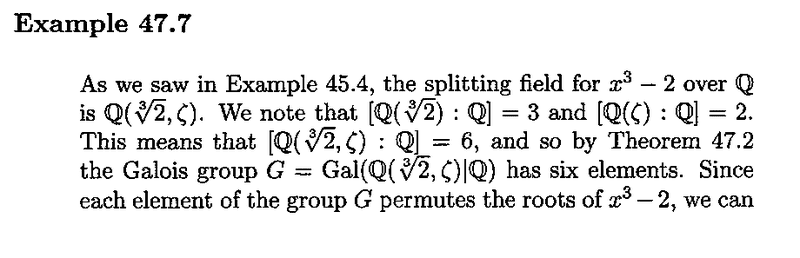
In the above example, Anderson and Feil write the following:

"... ... We note that $[ \mathbb{Q} ( \sqrt[3]{2} ) : \mathbb{Q} ] = 3$ and $[ \mathbb{Q} ( \zeta ) : \mathbb{Q} ] = 2$. ... ... "
Can someone please explain to me how/why $[ \mathbb{Q} ( \zeta ) : \mathbb{Q} ] = 2$ ... ... ?

Anderson and Feil give the definition of $\zeta$ in Chapter 9 in Exercise 25 ... as follows ... :

Hope someone can help ...

Peter

 

[andrewkirk]

Can someone please explain to me how/why $[ \mathbb{Q} ( \zeta ) : \mathbb{Q} ] = 2$ ... ... ?

$\zeta=e^{2\pi/3}=-\frac12 +i\frac{\sqrt 3}2$ so that $\zeta^2=-\zeta=1/\zeta$, and $\zeta^3=1$.

Hence every positive or negative integral power of $\zeta$ lies in $\{1,\zeta,-\zeta\}$ so that every element of $\mathbb Q(\zeta)$ can be written as $a+b\zeta$, where $a,b\in\mathbb Q$.

So a basis for $\mathbb Q(\zeta)$ as a vector space over $\mathbb Q$ is $\{1,\zeta\}$, so that the dimension of the VS is 2.

 

[mathwonk]

to answer your question, ask yourself how to find the dimension of the field generated by an element. hopefully you know it means to know the degree of the irreducible polynomial satisfied by that element. If not, master that fact. then ask yourself what irreducible polynomial is satisfied by a cube root of 1. I really recommend you try a little harder to answer these questions on your own. the key is to review the meaning of the terms in the question. here the key fact is that for an element a, the field F(a) is isomorphic to the quotient F[X]/(g) where g is the unique monic irreducible polynomial in F[X] satisfied by a. Hence a basis for that vector space over F is given by 1, X,...,X^n-1, where n = degree(g). This is fundamental.

 

[Math Amateur]

Thanks to Andrew and mathwonk for the help and advice ... ...

Now, following the advice provided by mathwonk, my reasoning is as follows:The polynomial satisfied by a cube root of $1$ is $x^3 - 1$ ... ... but this is not irreducible in $\mathbb{Q}$ since:

$x^3 - 1 = ( x - 1 ) ( x^2 + x + 1 )$If we focus on the irreducible polynomial $( x^2 + x + 1 )$ we find that the roots of this polynomial are

$\zeta = - \frac{1}{2} + \frac{ \sqrt{3} i }{ 2}$, and $\zeta^2 = - \frac{1}{2} - \frac{ \sqrt{3} i }{ 2}$ ...... so the degree of the minimum polynomial for $\zeta$ is $2$ ...

... and therefore $[ \mathbb{Q} ( \zeta) : \mathbb{Q} ] = 2$ ...Is the above reasoning correct?

Peter

 

[mathwonk]

That's perfect. Now ask yourself why you did not get this on your own. Clearly you can do this sort of thing. Maybe like me you just get impatient to know the answer and lose confidence that it will come to you. Because of the advice I gave you, I myself earlier today hung in a little longer on a problem that was bugging me in elementary algebraic geometry. I wanted to look at the solution online but reminded myself I had told you that one would be better off doing it oneself. so I kept at it, and I got it! you realize of course that computing the actual solutions is superfluous once you know two facts: the polynomial X^2+X+1 is irreducible, and has degree 2. Of course knowing the roots are complex IS one way to show it is irreducible. but you could also calculate the discriminant, see it is negative and stop there. nice work!