Gauss' law and the potential V (plane layer case)

[srnixo]

Homework Statement

I am completely unable to solve the second and third questions, can you please help and guide me?

Relevant Equations

.

Here is the exercise:

And these are my attempts:
This is for the first question about the electric field.
(I know I'm missing the drawing, which is a drawing of the plane layer of thickness 2e with a cylinder on it as a GAUSS SURFACE ).

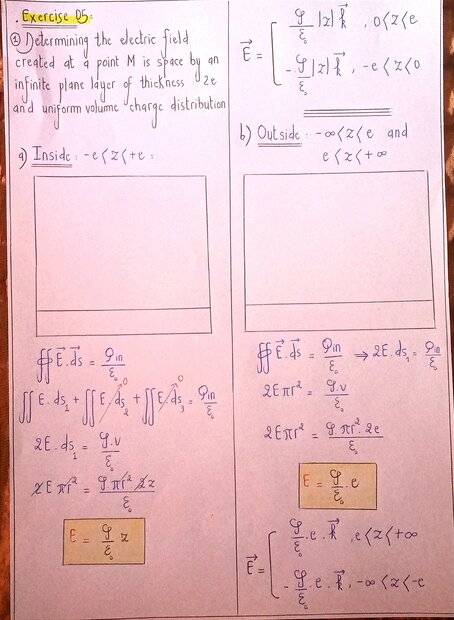
As for the second question, I'm not sure about it, so I asked for your help.

-> For the third question, I really can't draw the graphs, so I want to know the secret of drawing the graph, how do I know it is hyperbolic or linear or just a random shape etc... , because our professor in the previous exercises draws them directly without us understanding how, even when we ask her, she doesn't answer us. (please help).

 

[kuruman]

Your answers to the first question are fine.

In the second question, you find that inside the distribution you have $$V(M)=-\frac{\rho}{2\epsilon_0}z^2+C_1.$$That is correct so far. However, you need to find the constant of integration. Note that the problem says that you must choose $V=0$ at the median plane. You have not used this piece of information.

 

[srnixo]

Your answers to the first question are fine.

In the second question, you find that inside the distribution you have $$V(M)=-\frac{\rho}{2\epsilon_0}z^2+C_1.$$That is correct so far. However, you need to find the constant of integration. Note that the problem says that you must choose $V=0$ at the median plane. You have not used this piece of information.

When V=0 which implies z=0, the term z² in the expression for the potential inside the layer also becomes zero.
So, the potential V(M) inside the layer (-e < z < e) at z = 0, will be equal to zero? right?

 

[kuruman]

Right. So what should the expression for V(M) inside be?
What about outside? There should be no constants of integration because the zero of potential has already been defined for you.

 

[srnixo]

Right. So what should the expression for V(M) inside be?
What about outside? There should be no constants of integration because the zero of potential has already been defined for you.

For the inside, when choosing V=0 : the constant of integration C1 will indeed be 0 so the expression of V(M) inside will be : V(M)= -ρ. z²/2ε0

For the outside: we have two cases: above the plane layer z>e and below the plane layer z<-e :

→ for the first case which is above the plane layer z>e:
when calculating the constant of integration C2 we will find : C2 = ρ. e²/2ε0 and so, the expression of V(M) will be written as: V(M)= -ρ.e. z/ε0 +ρ. e²/2ε0

→ for the second case which is below the plane layer z<-e :
when calculating the constant of Integration C3 we will find : C3 = -3/2 .ρ . e²/ε0 , and so, the expression of V(M) will be : V(M) = ρ.e.z/ε0 -3/2 .ρ. e²/ε0

 

[kuruman]

You need to understand the the potential below and above the distribution must be the same. That's because the charge distribution is symmetric about the median plane. Check your algebra when you match the potential inside and outside below the plane at $z=-e.$

 

[srnixo]

You need to understand the the potential below and above the distribution must be the same.

But each time the constant of integration must be calculated, even if above or below the plane layer, the constant of integration is different and therefore the statement is different.

the first part of the potential expression for both ( above or below the plane layer is the same) which is V(M) = ρ.e.z/ε0 , but the second part about C2 and C3 (constants) are not the same isn't that correct?

 

[kuruman]

But each time the constant of integration must be calculated, even if above or below the plane layer, the constant of integration is different and therefore the statement is different.

the first part of the potential expression for both ( above or below the plane layer is the same) which is V(M) = ρ.e.z/ε0 , but the second part about C2 and C3 (constants) are not the same isn't that correct?

Yes, the calculation needs to be done above and below the plane. Did you do it correctly? Show me your calculation for below the plane, $z \leq -e$.

Please use LaTeX to make it legible. It's easy to learn. Just click on the link "LaTeX Guide" lower left above "Attach files".

I agree that the potential inside ($-e\leq z\leq+e$) is $V_{in}(z)=-\dfrac{\rho}{2\epsilon_0}z^2.$