Gauss' Law: Electric Field of Spherical Shell Insulator

[miniMitts27]

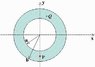
Given a spherical shell insulator as defined by an inner radius a = 4 cm and an outer radius b = 6 cm and carries a total charge of Q = + 9 C (1 C = 10-6 C). (You may assume that the charge is distributed uniformly throughout the volume of the insulator).
What is Ey, the y-component of the electric field at point P which is located at (x,y) = (0, -5 cm)? (picture of situation is attached)

Basically I just don't even know where to start. I realize that it's a Gauss' Law problem... I just don't know where to go from here. Any help would be greatly appreciated!

 

[oli4]

Hi miniMitts27
You are correct, whenever you see a problem like this with spherical symmetry, Gauss's theorem sounds like the weapon of choice.
So what does the theorem say (in your case) ?
You can draw a sphere centred on your shell's centre and passing through your point P
You know by symmetry that the field E will be radial and have everywhere the same magnitude
So just write Gauss's theorem with this particular surface and evaluate the integral which, thanks to this symmetry will allow you to take E outside and just evaluate the total charge inside the imaginary surface
Cheers...