sams
Gold Member
- 84
- 2
In Mathematical Methods for Physicists, Sixth Edition, Page 60, Section 1.11, the Gauss' theorem is written as:
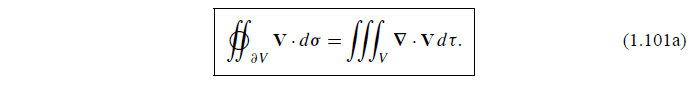
In Mathematical Methods for Physicists, Fifth Edition, Page 61, Section 1.11, the Gauss' theorem is written as:
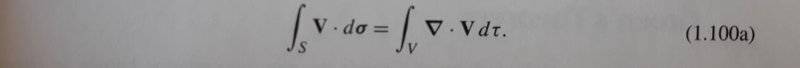
Kindly I would like to know please:
1. What is the difference between the two relations?
2. What does ##\partial{V}## in Equation (1.101a) stands for? In physics, I realized that ##\partial{V}## is usually not included when Gauss' theorem is used, why is that?
Thanks a lot for your help...
In Mathematical Methods for Physicists, Fifth Edition, Page 61, Section 1.11, the Gauss' theorem is written as:
Kindly I would like to know please:
1. What is the difference between the two relations?
2. What does ##\partial{V}## in Equation (1.101a) stands for? In physics, I realized that ##\partial{V}## is usually not included when Gauss' theorem is used, why is that?
Thanks a lot for your help...
Attachments
Last edited by a moderator: