General Question about Vibrations

[tomadevil]

Hello Everyone,

I conducted an experiment with a metal beam which had a motor attached to it in with an eccentric mass on it. The two ends of the beams were fixed with a roller and a hinge(as I remember). This was a one degree of freedom experiment.

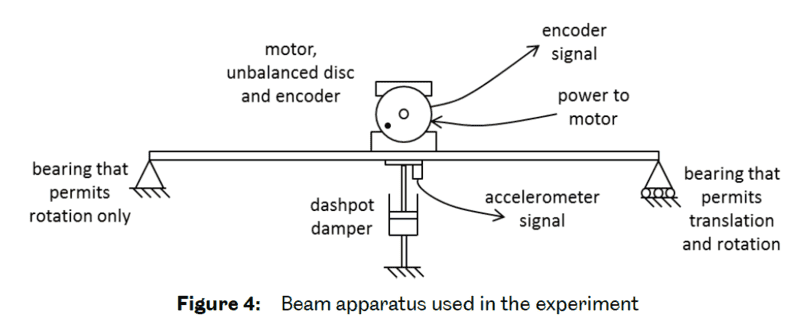
I had to collect data during free/forced and damped/undamped vibrations. My data clearly shows that the resonance frequency is higher than the natural frequency but I don't really know why. I believe they should be the same.
I was thinking it might be related to the fact that this is a rotating system. Am I on the right track?
Can someone explain to me what causes this difference?

Thank you for the answer.
Thomas

 

[anorlunda]

That sounds like an interesting experiment.

Can you show us how you calculated the natural frequency?

 

[tomadevil]

I used the half power method to work out zeta for the forced vibration. Then, I worked out the natural frequency with the following equations:
http://www.kepfeltoltes.eu/view.php?filename=562vib.png

In the case of the free vibration, the logarithmic decrement, damping ratio were found, then the natural frequency:
http://www.kepfeltoltes.eu/view.php?filename=619equ.png

 

[anorlunda]

What about the mass, shape and position of the motor, brackets and the mass? Did you include those in the natural frequency calculation?

 

[tomadevil]

What about the mass, shape and position of the motor, brackets and the mass? Did you include those in the natural frequency calculation?

No, I didn't. We have to assume that the motor is exactly in the middle of the beam and I think that would be beyond the scope of this exercise.

 

[anorlunda]

I asked that because the mass of the motor would probably change the natural frequency. Attach a large mass to a tuning fork and the pitch of the sound changes. The natural frequency of the shaft and the natural frequency of the system are not necessarily the same.

Your original question was why experiment does not agree with calculation. So you are seeking something wrong with your calculation.

 

[JBA]

The test frequency being higher than the calculated would indicate that possibly either the mass of the system is lighter than that used in your calculation or that the actual damping factor is less than your calculated one.

 

[Dr.D]

If the actual system looks like your sketch above, then the motor is almost certainly the most significant mass in the system.

In truth, this is a system with infinitely many degrees of freedom. To say that it is 1 DOF involves a significant approximation, but it may be useful.

The expression you have relating the resonant frequency to the natural frequency must always give the resonant frequency higher than the natural frequency. You are calculating the resonance frequency by dividing the natural frequency by a number less than 1.0. I think you have some factors mis-arranged.