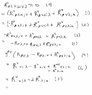General relativity. Bianchi identities

In summary, the conversation is about a problem in proving that the divergence of Einstein tensor is 0 using the bianchi identities. The person has looked at several sources and derived an answer, but still has some questions about certain steps. They are specifically asking about how to get from eq2 to eq3 and how to distribute the metric in equation 5 to get eq6. They are also seeking help in understanding how the covariant derivative affects the index's raising.
  • #1
TheSource007
15
0

Homework Statement



I have a problem. I need to prove that the divergence of Einstein tensor is 0 using the bianchi identities. I have looked to several sources and I have derived an answer, but I don't fully understand some steps.

Homework Equations


I have uploaded a document which shows a part of the solution, because I have no idea hot to write them in the post. The solution starts with eq0.
I don't understand how did they get from eq 2 to eq 3. It seems like some sort of contraction in the index a and u, but what kind or rule/law/equation is that? If it's a contraction between first and third slots, why didnt they contract also the third term in eq 2?
My second question is, when raising an index, how the metric in equation 5 is distributed to get eq6? It seems that the metric is distributed like simple algebra. Why is it like that? How the covariant derivative affect the index's raising.
If you can help me with those two questions, then I will be able to understand the rest.
Please be kind since I am very new at this stuff. The book I am using is gravitation by misner thorne wheeler.

The Attempt at a Solution

 

Attachments

  • E. Tensor.jpg
    E. Tensor.jpg
    24.9 KB · Views: 1,289
Physics news on Phys.org
  • #2
I have attempted to answer the questions by looking at various sources. However, I am still not sure how to answer them.
 

FAQ: General relativity. Bianchi identities

1. What is general relativity?

General relativity is a theory of gravitation that was developed by Albert Einstein in the early 20th century. It describes how massive objects interact with each other and how they affect the geometry of space and time.

2. How does general relativity differ from Newton's theory of gravity?

Unlike Newton's theory, which describes gravity as a force between objects, general relativity explains gravity as the curvature of space and time caused by the presence of massive objects. It also takes into account the effects of acceleration and the speed of light.

3. What are the Bianchi identities in general relativity?

The Bianchi identities are a set of mathematical equations that describe the behavior of the curvature of space and time in general relativity. They are used to ensure that the theory is consistent and to derive other important equations, such as the Einstein field equations.

4. How do the Bianchi identities relate to the conservation of energy and momentum?

The Bianchi identities are closely related to the conservation of energy and momentum in general relativity. They show that energy and momentum are conserved in a region of spacetime if the curvature of spacetime is invariant within that region.

5. What are some practical applications of general relativity and the Bianchi identities?

General relativity has many practical applications, such as predicting the orbits of planets and satellites, understanding the behavior of black holes, and helping to improve the accuracy of GPS systems. The Bianchi identities are used in the field of cosmology to study the large-scale structure and evolution of the universe.

Similar threads

Prove v<c for particles with m>0 using two identities
Replies
8
Views
201
Contraction of the Bianchi identity
Replies
2
Views
2K
A body at rest in Doran and Boyer-Lindquist coordinates
2
Replies
46
Views
2K
General relativity - Using Ricc and Weyl tensor to find the area
Replies
1
Views
1K
I Strange result from Bianchi identity, me spot the error
Replies
13
Views
1K
Deriving equation 9.91 in Carroll's Book "Spacetime and Geometry"
Replies
1
Views
1K
Understanding Green's second identity and the reciprocity theorem
Replies
3
Views
4K
Electromagnetic dual tensor. General Relativity
Replies
4
Views
4K
A problem Sean Carroll's book about Killing vectors
Replies
1
Views
3K
General relativity- Coordinate/metric transformations
Replies
3
Views
2K

Hot Threads

Recent Insights

Back
Top