cg78ithaca
- 14
- 1
I am aware that hypergeometric type differential equations of the type:
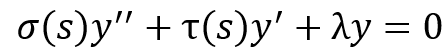
can be solved e.g. by means of Mellin transforms when σ(s) is at most a 2nd-degree polynomial and τ(s) is at most 1st-degree, and λ is a constant. I'm trying to reproduce the method for the case where λ is not constant, but a 3rd-degree polynomial, and I'm not sure how to solve Mellin-transformed version of the equation above if λ is a polynomial and not a constant, if indeed it is solvable analytically.
Does the equation above have analytical solutions if λ(s) is a 3rd-degree polynomial, and if so, how do I arrive at them?
can be solved e.g. by means of Mellin transforms when σ(s) is at most a 2nd-degree polynomial and τ(s) is at most 1st-degree, and λ is a constant. I'm trying to reproduce the method for the case where λ is not constant, but a 3rd-degree polynomial, and I'm not sure how to solve Mellin-transformed version of the equation above if λ is a polynomial and not a constant, if indeed it is solvable analytically.
Does the equation above have analytical solutions if λ(s) is a 3rd-degree polynomial, and if so, how do I arrive at them?