Geometry and algebraic equations

[member 428835]

Hi PF!

I'm given a circle with parametric representation $x=r\sin\theta,y=h+r\cos\theta$. There is also a line, which has the parametric equation $x=x,y=\cot (\beta) x$. Note the line makes angle $\beta$ with the y-axis. When the circle intersects the line, it makes an angle, call this angle $\alpha$. The 2D area of the enclosed y-axis,circular arc, and line, together form an area, call this $A$. Given $\beta,\alpha,A$, I want to determine $h,r,\theta_e$ where $\theta_e$ is the $\theta$ value that intersects with the line. See the image below for clarity.

I've come up with three equations to specify the system: can you confirm these are correct? I use subscribts $c$ and $l$ to denote circle and line respectively.

1) area equation
$$
\int_0^{\theta_e} y_c \, dx - \int_0^{x_c(\theta_e)} y_l \, dx = A \implies\\
\int_0^{\theta_e} y_c x_c'(\theta) \, d\theta - \int_0^{x_c(\theta_e)} y_l \, dx = A \implies\\
\boxed{\frac{1}{2} r (\sin (\theta_e ) (2 h+r \csc (\beta ) \sin (\beta -\theta_e))+\theta_e r) = A}.
$$

2) circle intersecting line equation
$$
x_c = x_l,\,\,\,y_c=y_l\implies\\
\boxed{h+r\cos\theta_e = r\sin\theta_e\cot\beta}.
$$

3) dot product of unit-tangent vectors for circle and line intersection must equal $\cos\alpha$

$$
\left.\frac{\langle x_c'(\theta),y_c'(\theta)\rangle}{|| \langle x_c'(\theta),y_c'(\theta)\rangle||} \cdot \frac{\langle x_l,y_l'(x)\rangle}{|| \langle x_l,y_l'(x)\rangle||}\right|_{\theta=\theta_e} = \cos\alpha\implies\\
\boxed{-\sin(\theta_e-\beta)=\cos\alpha}.
$$

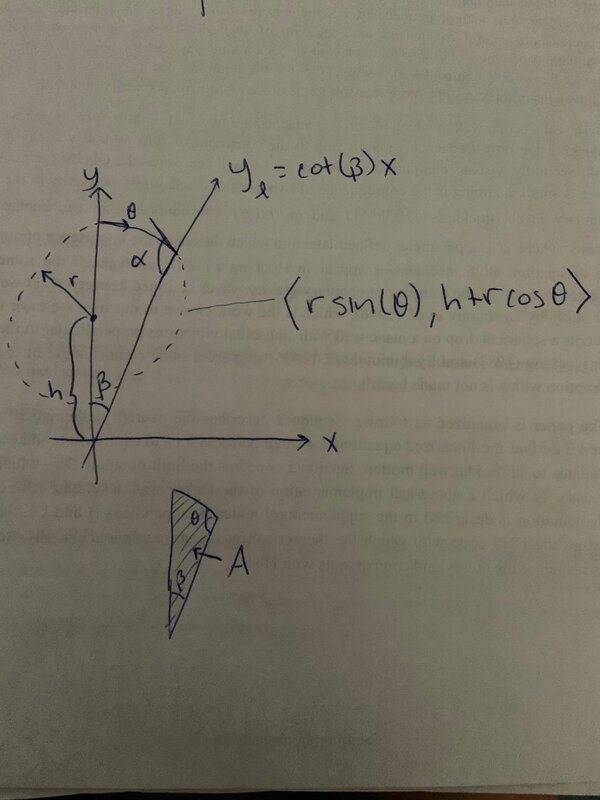
How do these equations look? (OOPS, the bottom figure labels the upper-right angle $\theta$, but it should read $\alpha$. My fault!)

 

[Charles Link]

I didn't look over everything, but most of it looks good. I do see in the dot product with the line that goes through the origin, you can either use $(x,y)$ or $(1,dy/dx)$, but not $(x, dy/dx)$.
e.g. You can parametrize the line with $x=x$ and $y=y(x)$, and instead of using $(dx/dt,dy/dt)$, you use $(dx/dx,dy/dx)$ for the tangent vector.

 

[member 428835]

I didn't look over everything, but most of it looks good. I do see in the dot product with the line that goes through the origin, you can either use $(x,y)$ or $(1,dy/dx)$, but not $(x, dy/dx)$.
e.g. You can parametrize the line with $x=x$ and $y=y(x)$, and instead of using $(dx/dt,dy/dt)$, you use $(dx/dx,dy/dx)$.

Shoot, I meant 1 there ***typo***, so dx/dx. Thanks. So this is correct: I'm not crazy?

 

[Charles Link]

It looks very good, but I did not yet study it in enough detail to verify whether it is completely correct. I think you did a couple of things rather well, including getting the direction and position of $\theta$ correct.

 

[member 428835]

Thanks. See when I solve there are some tricky parts. For example, the arc can be convex or concave. Anyone see anything tricky I'm missing?