Geometry of Cherenkov radiation

[AndreasC]

As an explanation to the Cherenkov angle, images such as this are offered:

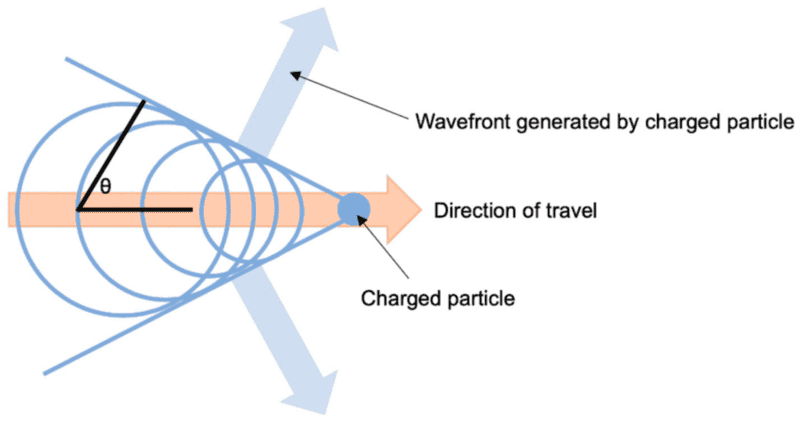
This is used to explain the Cherenkov angle θ at which the Cherenkov radiation appears to be propagating. To figure this angle out however one has to assume that the wavefronts are tangent to each of these circles, so that then the direction of propagation and the observed wavefronts have a right angle between them. I don't really get why. I think I'm missing something very obvious, and it probably has to do with interference, but I can't quite explain it.

To be more specific, take a point where that first circle meets the wavefront. If you wait just a little bit, won't the emitted radiation from the second circle reach that point? Won't it then appear to be coming from a different angle?

 

[vanhees71]

This is using the Huygens's Principle for emission of waves with velocity $c_{\text{mat}}=c/n$ by a charge moving with a velocity larger than $c_{\text{mat}}$.

 

[AndreasC]

This is using the Huygens's Principle for emission of waves with velocity $c_{\text{mat}}=c/n$ by a charge moving with a velocity larger than $c_{\text{mat}}$.

I'm not entirely sure how this applies to answer what I said in the end though... I'm also not entirely sure why all the points in that tangent line have the same phase. Perhaps that's why I'm confused.

 

[AndreasC]

Wait I see what you mean now about Huygens' principle, but where I'm stuck I guess is why these points are a wavefront, as in why do these points along this line have the same phase, but not some other ones? I think I've misunderstood the nature of radiation being emitted from the electron...

 

[AndreasC]

Oof nevermind, I was saying nonsense because I was confused. I see what you mean now, thanks!