Geometry Problem #90: Arc vs. Chord Distance on a Semicircular Path

[Jameson]

This is for beginning geometry students so if you are new to geometry, take a look! :)

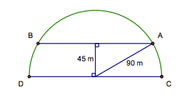
Marcia could walk from A to B along arc AB on the semicircular path, or she can walk along
chord AB. Diameter CD has length 180m. How much farther is it to walk along the arc as
opposed to the chord?

View attachment 1772
--------------------

 

[Jameson]

This problem came from The Art of Problem Solving (AoPS) website.

Congratulations to the following members for their correct solutions:

1) MarkFL
2) mente oscura
3) anemone
4) eddybob123

Solution (from MarkFL):

Spoiler

Please consider the following diagram:

From this we find:

$$\cos(x)=\frac{\frac{r}{2}}{r}=\frac{1}{2}\implies x=\frac{\pi}{3}$$

Hence, arc $AB$ (denoted by $s$) has length:

$$s=r(2x)=\frac{2\pi r}{3}$$

Line segment $\overline{AB}$ may be found from:

$$\sin(x)=\frac{\frac{1}{2}\overline{AB}}{r}$$

$$\overline{AB}=2r\sin(x)=\sqrt{3}r$$

Thus, the difference $\Delta$ between the two paths is:

$$\Delta=s-\overline{AB}=\frac{2\pi r}{3}-\sqrt{3}r=\frac{r}{3}\left(2\pi-3\sqrt{3} \right)$$

Using the given data:

$$r=90\text{ m}$$

we have:

$$\Delta=30\left(2\pi-3\sqrt{3} \right)\text{ m}$$