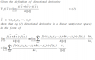Undergrad Gradient Derivation: Simplifying Directional Derivatives
- Thread starter kidsasd987
- Start date
-
- Tags
- Derivation Gradient
Click For Summary
The discussion focuses on the derivation of the directional derivative, emphasizing its geometric interpretation as the rate of change of a function along a specific basis vector. It explains that derivatives can be calculated with respect to arbitrary vectors, requiring the projection of the function onto that vector. The process involves using inner products to find the relevant components, including subtracting the perpendicular component and possibly normalizing the projection vector. The conversation highlights the importance of limits in defining the gradient with respect to the chosen direction. Overall, the thread clarifies the mathematical foundations necessary for understanding directional derivatives.
Similar threads
- · Replies 8 ·
- · Replies 18 ·
- · Replies 4 ·
- · Replies 4 ·
- · Replies 14 ·
- · Replies 8 ·
- · Replies 5 ·
- · Replies 38 ·