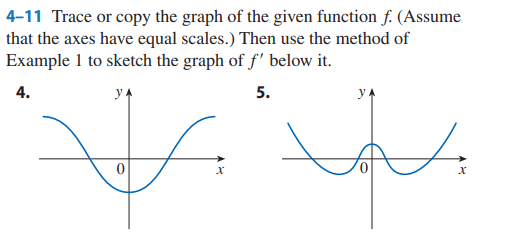Homework Help Overview
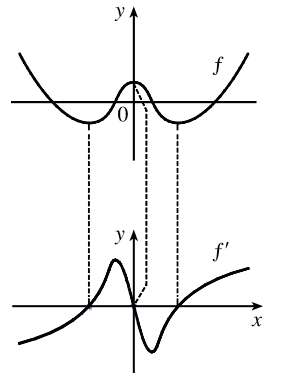
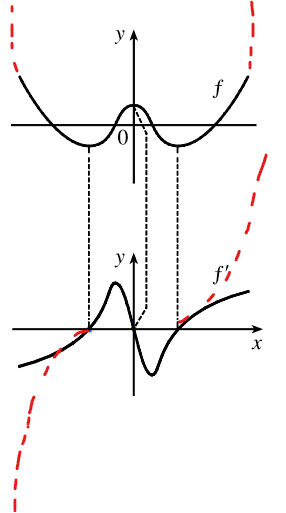
The discussion revolves around the graphical representation of the derivative function f' in relation to the original function f, specifically focusing on the end behavior and characteristics of these graphs. Participants are analyzing the implications of changes made to the graph of f' and how these relate to the properties of f.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants are questioning the accuracy of altered graphs of f' and discussing the implications of steepness and asymptotic behavior. There are attempts to clarify the relationship between the order of the functions and their derivatives, as well as the effects of gradient changes on the graph.
Discussion Status
The discussion is ongoing, with participants providing insights and questioning each other's interpretations. Some guidance has been offered regarding the estimation of derivatives through graphical methods, but no consensus has been reached on the correctness of the graphs presented.
Contextual Notes
Participants are navigating assumptions about the nature of the functions involved, including their orders and behaviors at extremes. There is mention of homework constraints that may limit the exploration of certain aspects of the problem.