Gravitational Plot: Accuracy Checked
- Context: Undergrad
- Thread starter Invutil
- Start date
-
- Tags
- Gravitational Plot
Click For Summary
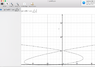
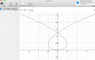
The discussion centers on the accuracy of gravitational motion equations, specifically addressing the use of constant acceleration formulas in variable force scenarios. The equations presented include x(t) = x0 + v0 t + 1/2 a t^2 and F = G m1 m2 / r^2, with emphasis on their applicability in planetary motion versus free fall. Participants highlight the complexity of planetary motion equations, which lead to second-order differential equations and relate to Kepler's laws. The consensus is that numerical integration is necessary for accurate modeling of motion under variable gravitational forces.
PREREQUISITES- Understanding of Newton's laws of motion
- Familiarity with gravitational force equations, specifically F = G m1 m2 / r^2
- Knowledge of differential equations and their application in physics
- Experience with numerical integration techniques for solving motion equations
- Study the derivation and implications of Kepler's laws of planetary motion
- Learn about numerical integration methods for solving differential equations in physics
- Explore the differences between constant and variable acceleration in gravitational contexts
- Investigate the implications of negative radius values in gravitational equations, particularly in relation to Kerr black holes
Physics students, astrophysicists, and engineers involved in gravitational modeling and simulation, particularly those focusing on planetary motion and free-fall dynamics.
Similar threads
- · Replies 10 ·
- · Replies 19 ·
- · Replies 9 ·
- · Replies 6 ·
- · Replies 10 ·
- · Replies 2 ·
- · Replies 11 ·
- · Replies 1 ·
- · Replies 27 ·
- · Replies 15 ·