Amaelle
- 309
- 54
- Homework Statement
- Look at the image
- Relevant Equations
- Green theorem
circuitation
Greetings!
My question is: is it possible to use the green theorem to compute the circulation while in presence of a scalar function ? I know how to solve by parametrising each part but just in case we can go faster? thank you!
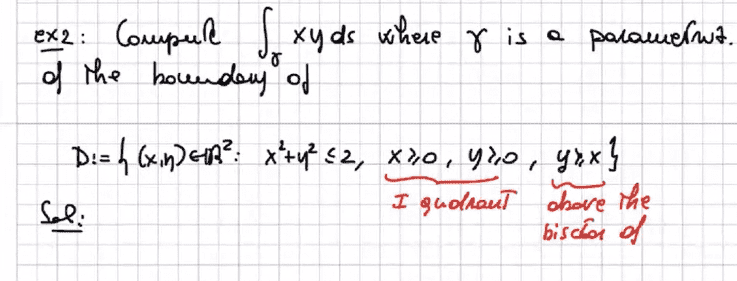
My question is: is it possible to use the green theorem to compute the circulation while in presence of a scalar function ? I know how to solve by parametrising each part but just in case we can go faster? thank you!