Cibek
- 13
- 0
Hello!
I have recently been looking into the phenomenon of gyroscopic precession in my free time, and there is a scenario which I am not sure I have fully understood. Here it is:
Imagine a bicycle wheel with a shaft running through it's center. The shaft is attached to a rope at one of it's sides, and is held upright before it is spun up. If the wheel was not spinning, the force of gravity would simply cause the wheel to start swinging around the attachment point of the rope. However, when the wheel is spinning gyroscopic precession will cause the wheel to stay upright and instead start rotating around the rope, in the horizontal direction. This is supposedly because a force applied to a spinning object acts 90 degrees from the direction it was applied, which in this case causes the wheel to start rotating around the rope.
My questions are:
Is the precession occurring because the wheel is starting to change alignment when it starts swinging, and therefore the gravitational force is applied at an angle? In that case, am I right in assuming that the rotation would not start while the wheel is completely verticly upright? Or can a completely upright wheel still precess and rotate?
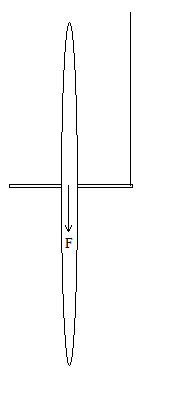
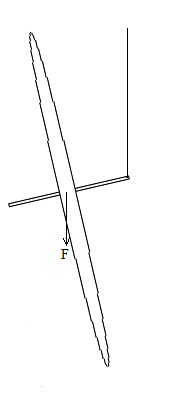
I have recently been looking into the phenomenon of gyroscopic precession in my free time, and there is a scenario which I am not sure I have fully understood. Here it is:
Imagine a bicycle wheel with a shaft running through it's center. The shaft is attached to a rope at one of it's sides, and is held upright before it is spun up. If the wheel was not spinning, the force of gravity would simply cause the wheel to start swinging around the attachment point of the rope. However, when the wheel is spinning gyroscopic precession will cause the wheel to stay upright and instead start rotating around the rope, in the horizontal direction. This is supposedly because a force applied to a spinning object acts 90 degrees from the direction it was applied, which in this case causes the wheel to start rotating around the rope.
My questions are:
Is the precession occurring because the wheel is starting to change alignment when it starts swinging, and therefore the gravitational force is applied at an angle? In that case, am I right in assuming that the rotation would not start while the wheel is completely verticly upright? Or can a completely upright wheel still precess and rotate?