Hawking Radiation and Shrinking Black Holes

[Robert Friz]

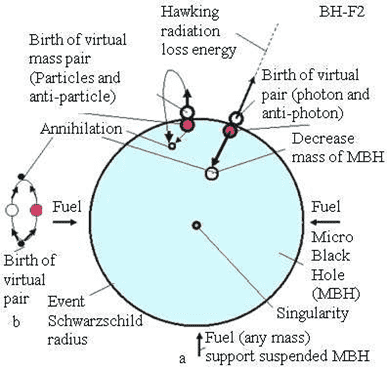
Stephen Hawking theorized the creation of virtual particle pairs at the event horizon of a black hole, with one of the particles escaping the event horizon (Hawking Radiation) and the other particle falling into the black hole.

Sean Carroll states on page 272 of From Eternity to Here that "if the real particle that escapes the black hole has positive energy, and the total energy of the original virtual pair was zero, that means the partner that fell into the black hole must have negative energy. When it falls in, the total mass of the black hole goes down." Mr. Carroll (whose work I highly respect) goes on in the following paragraph to conclude that, based on this theory, the resulting loss of mass from the black hole will eventually result in it evaporating entirely.

However, I believe that it is equally likely that the virtual particle that falls into the black hole will be a positive energy virtual particle and the negative energy virtual particle will escape the event horizon. If that is true, then the net result of many instances of one of two virtual particles falling into the black hole will be zero change to the mass of the black hole.

Theoretically what is going on here? Whose thinking is faulty? My thoughts (most likely)? Sean Carroll's writing (unlikely)? Stephen Hawking's research (highly unlikely)?

Diagrams of this phenomenon usually picture only the anti-photon falling into the black hole, as pictured in the researchgate.net diagram below:

https://www.physicsforums.com/file:///C:/Users/Bob%20HP%20Laptop/AppData/Local/Temp/msohtmlclip1/01/clip_image001.jpg

 

[phinds]

Hawking said that the "virtual particle" description of what is now called Hawking Radiation is ONLY a heuristic and is absolutely not to be taken literally. He said it was just the best he could do to express in the the English language something that really can only be expressed in the math.

Why Carroll promulgates the heuristic as though it were a literally correct description of the physics is beyond me. Maybe he is just playing with the heuristic or maybe (unlikely) he just isn't aware of the actual phenomenon's correct description.

 

[Robert Friz]

Hawking said that the "virtual particle" description of what is now called Hawking Radiation is ONLY a heuristic and is absolutely not to be taken literally. He said it was just the best he could do to express in the the English language something that really can only be expressed in the math.

Why Carroll promulgates the heuristic as though it were a literally correct description of the physics is beyond me. Maybe he is just playing with the heuristic or maybe (unlikely) he just isn't aware of the actual phenomenon's correct description.

Interesting. Thank you.

 

[PeroK]

However, I believe that it is equally likely that the virtual particle that falls into the black hole will be a positive energy virtual particle and the negative energy virtual particle will escape the event horizon. If that is true, then the net result of many instances of one of two virtual particles falling into the black hole will be zero change to the mass of the black hole.

The particle that escapes the black hole cannot have negative energy to an external observer. That is not possible. That particle must have positive energy.

But, using something of a mathematical trick at the event horizon of the black hole, the particle that falls into the black hole reduces the energy of the black hole. The trick is based on the fact that a certain Killing vector is timelike outside the event horizon and spacelike inside. It's the reversal of the Schwarzschild coordinate $r$ from spacelike oustide the horizon to timelike inside the horizon on which the positive/negative energy of the particles is based. In other words, the particle energies depend on the unique properties of spacetime at the event horizon.

This is where a little mathematical medicine helps!

In any case, whatever particle of the pair escapes has positive energy.

 

[Robert Friz]

The particle that escapes the black hole cannot have negative energy to an external observer. That is not possible. That particle must have positive energy.

But, using something of a mathematical trick at the event horizon of the black hole, the particle that falls into the black hole reduces the energy of the black hole. The trick is based on the fact that a certain Killing vector is timelike outside the event horizon and spacelike inside. It's the reversal of the Schwarzschild coordinate $r$ from spacelike oustide the horizon to timelike inside the horizon on which the positive/negative energy of the particles is based. In other words, the particle energies depend on the unique properties of spacetime at the event horizon.

This is where a little mathematical medicine helps!

In any case, whatever particle of the pair escapes has positive energy.

Thank you. My head hurts... LOL

 

[kimbyd]

Why Carroll promulgates the heuristic as though it were a literally correct description of the physics is beyond me. Maybe he is just playing with the heuristic or maybe (unlikely) he just isn't aware of the actual phenomenon's correct description.

He's a good theorist. He probably thought that it was accurate enough for a lay audience. I'm not sure the realistic descriptions are very accessible to non-experts.

 

[kimbyd]

Thank you. My head hurts... LOL

The math here is really really weird.

Wikipedia has a good derivation:
https://en.wikipedia.org/wiki/Hawking_radiation#Emission_process

The basic logic is:
1) Consider what an observer right outside a black hole would see. In order to remain outside the black hole, they have to be accelerating outward. Accelerating observers in General Relativity see radiation, which is known as the Unruh effect.
2) For this to be observed, the observer near the horizon has to be bathed in radiation. Redshift this radiation out to infinity, and get the temperature of the black hole as observed far away.

This argument suggests that the curvature of space-time itself just outside the black hole produces radiation. Because General Relativity conserves the stress-energy tensor, this outgoing radiation carries energy away from the black hole, which means the black hole loses energy, which means it loses mass.

 

[Robert Friz]

The math here is really really weird.

Wikipedia has a good derivation:
https://en.wikipedia.org/wiki/Hawking_radiation#Emission_process

The basic logic is:
1) Consider what an observer right outside a black hole would see. In order to remain outside the black hole, they have to be accelerating outward. Accelerating observers in General Relativity see radiation, which is known as the Unruh effect.
2) For this to be observed, the observer near the horizon has to be bathed in radiation. Redshift this radiation out to infinity, and get the temperature of the black hole as observed far away.

This argument suggests that the curvature of space-time itself just outside the black hole produces radiation. Because General Relativity conserves the stress-energy tensor, this outgoing radiation carries energy away from the black hole, which means the black hole loses energy, which means it loses mass.

Excellent summary. Thank you. In a nutshell, my assumption is that the outgoing radiation is the primary reason for the loss of mass. Finally, I would not want to be responsible for guaranteeing that ANY virtual particle escapes the local black hole system. Either annihilation or gobbling certainly must occur in virtually (sorry) 100% of the cases where virtual particles (some of which become "real") are created.

 

[rootone]

The math here is really really weird.

Well it's not that weird if you consider that a velocity of less than zero is nonsense.

 

[phinds]

@Robert Friz you might be interested in

https://www.physicsforums.com/insights/physics-virtual-particles/
https://www.physicsforums.com/insights/misconceptions-virtual-particles/

 

[PeterDonis]

I would not want to be responsible for guaranteeing that ANY virtual particle escapes the local black hole system.

The particles that are observed as Hawking radiation are not virtual; they're real.

Sean Carroll states on page 272 of From Eternity to Here

Bear in mind that this is not a textbook or a peer-reviewed paper. It is a pop science book. Even when written by scientists who are knowledgeable about the field they are writing about, pop science books are not good sources if you actually want to learn the science. At best they will give you some references in their bibliography to actual works of science (textbooks or peer-reviewed papers).

 

[PeterDonis]

The basic logic is:
1) Consider what an observer right outside a black hole would see. In order to remain outside the black hole, they have to be accelerating outward. Accelerating observers in General Relativity see radiation, which is known as the Unruh effect.
2) For this to be observed, the observer near the horizon has to be bathed in radiation. Redshift this radiation out to infinity, and get the temperature of the black hole as observed far away.

Heuristically the logic is often presented this way, but it has a flaw: "acceleration radiation" (the Unruh effect) is observer-dependent: only accelerated observers see it. An observer free-falling into the hole would see no radiation. But the evaporation of a black hole by Hawking radiation is not observer-dependent: observers free-falling towards the hole would (in principle) see its mass decrease.

A more global view of what is going on goes something like this: we first find a quantum field state in curved Schwarzschild spacetime that is a vacuum state with respect to modes coming in from past null infinity. (Heuristically, there is no radiation coming in from infinity; the black hole is isolated in this respect.) We then ask what this state looks like with respect to modes going out to future null infinity, taking into account the "scattering" of the field modes by the curved spacetime. It turns out that with respect to modes going out to future null infinity, this state looks like a thermal state with temperature proportional to the hole's surface gravity (i.e., inversely proportional to its mass). The mathematical derivation of this result has nothing whatever to do with "virtual particles" since it's not even done in perturbation theory to begin with.

John Baez has some good comments on this here:

http://math.ucr.edu/home/baez/physics/Relativity/BlackHoles/hawking.html

A much more technically detailed reference is Wald's 1993 monograph Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics.

 

[Nugatory]

And Hawking's paper: https://projecteuclid.org/download/pdf_1/euclid.cmp/1103899181